Je voudrais continuer mes études sur les méthodes numériques parce que je les trouvais très précieux surtout parce qu’elles m’aideraient à comprendre les calculs impliqués quand j’apprends d’autres sujets comme la physique, d’autant plus que les maths et la physique sont très proches.
Le but de cette semaine est de comprendre la méthode ‘la plus utilisée’ — Runge Kutta d’ordre 4 (RK4). Ainsi, nous apprendrons quelques méthodes pour voir la raison pour laquelle certains d’entre elles estiment mieux que d’autres (sans plonger à fond dans les maths impliquées). Enfin, nous pouvons coder chacune en C et créer des graphiques linéaires pour pouvoir voir ces différences de performances.
La méthode du point milieu, ou Runge Kutta d’ordre 2 (RK2)
Il faut nous rappeler que pour les exemples suivants, on s’intéresse aux problèmes de Cauchys, où l’on utilise une équation différentielle avec une condition initiale :
où t0, T, et y0 sont donnés.
La méthode du point milieu (RK2), est un bon exemple d’étudier pour faire comprendre comment on peut dériver une méthode plus précise (par rapport à la méthode d’Euler) avec juste un peu plus de complexité. On verra pourquoi c’est le cas dans une prochaine leçon (spoiler : c’est grâce à des termes d’erreur d’ordre supérieur, et donc à des erreurs de troncature de la série de Taylor plus petites).
L’équation est sous la forme :
où, k2 se calcule :
k2 est la pente à … ainsi le nom de la méthode ‘du point milieu’. Si l’on compare la méthode d’Euler et cette méthode, on dirait que la méthode d’Euler utilise la pente à t0 tandis que la méthode du point milieu utilise la pente à .
Cependant, une question se pose :
Comment trouver la pente au temps ?
Les étapes sont les suivantes:
- Trouvez la pente k1 avec la méthode d’Euler à t0.
- Utilisez k1 pour estimer la solution de la fonction .
- Trouvez la nouvelle pente k2 avec la méthode d’Euler à .
- Revenez au début (où t = t0) et utilisez k2 avec la méthode d’Euler pour estimer la fonction y(t0 + h).
Je vous propose de regarder cette partie de cette ressource parce qu’elle a des graphiques utiles ainsi que des dérivations serviables. Ce lien vous offre aussi les calculs complets.
Runge Kutta d’ordre 4 (RK4)
Cette méthode est considérée comme — et je cite l’auteur du livre Numerical Recipes in C :
Runge-Kutta est ce que vous utilisez lorsque vous ne savez pas mieux, ou… vous avez un problème trivial où l’efficacité de calcul ne vous concerne pas. Runge-Kutta est très fiable et réussira toujours.
Comme nous le verrons, l’équation suivante est assez verbeuse, mais avec un peu d’intuition, elle est assez facile à comprendre. Cette fois-ci, on prend quatre estimations de la pente à chaque pas de temps pour mieux estimer l’approximation de la trajectoire de la courbe. Cette méthode est la plus précise entre les méthodes dont on a discuté dans cette série jusqu’à présent.
L’équation est la suivante :
où sont des pentes calculées à des points différents. Ils sont calculés comme suit :
Encore une fois, veuillez regarder ce lien ce lien sur RK4 pour que vous compreniez mieux la méthode… mais si vous comprenez la méthode du point milieu… ces équations ne vous semblent probablement pas si étrangères.
Implémentation en langage C et une comparaison entre nos méthodes :
J’ai écrit un programme en C qui peut nous aider à voir le comportement et le résultat pour chaque méthode. J’ai choisi l’équation différentielle et notre condition initiale :
Ce qui correspond à la solution analytique : et
Le programme écrit des données aux fichiers qui peuvent être utilisé pour qu’on puisse appeler gnuplot avec la commande plot 'midpoint.txt' w l, 'euler.txt' w l, 'rk4.txt' w l.
En utilisant un petit pas de temps h (ici, j’ai choisi 0,025), les trois méthodes sont quasi-égales :
| Méthode | h | tf | yf |
|---|---|---|---|
| Euler | 0,025 | 2,0 | 7,210 |
| Midpoint | 0,025 | 2,0 | 7,388 |
| RK4 | 0,025 | 2,0 | 7,389 |
| Analytique (et) | 2,0 | 7,389 |
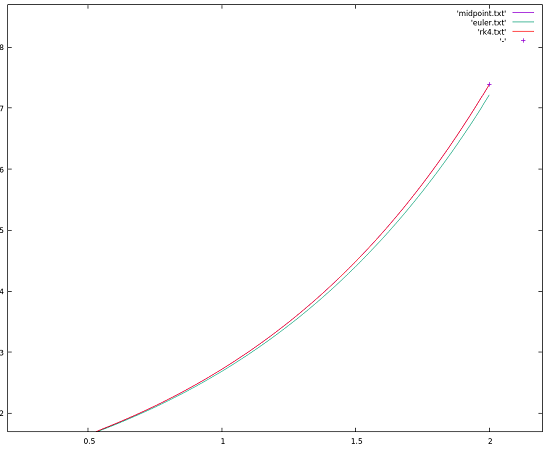
Ce qui est marquant, c’est quand nous réduisons le pas de 0,025 à 1,0 :
| Méthode | h | tf | yf |
|---|---|---|---|
| Euler | 1,0 | 2,0 | 4,0 |
| Midpoint | 1,0 | 2,0 | 6,25 |
| RK4 | 1,0 | 2,0 | 7,34 |
| Analytique (et) | 2,0 | 7,389 |
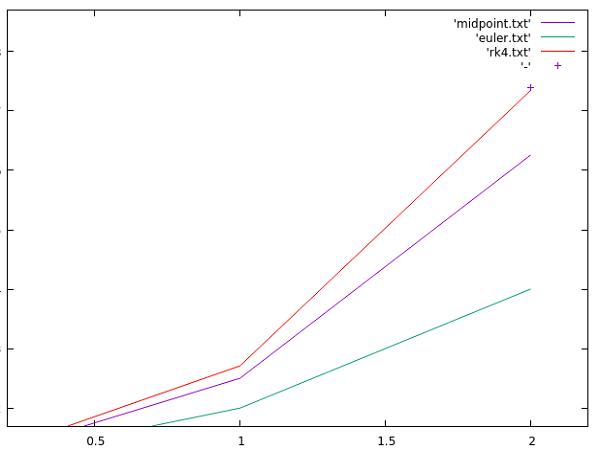
En comparant les trois méthodes dont nous avons parlé jusqu’ici, il est clair que même si la méthode RK4 prend quatre fois plus d’étapes pour estimer une solution à chaque pas de temps Δt ou h, elle peut prendre des pas de temps beaucoup plus longs pour se rapprocher de la valeur réelle, ce qui peut la rendre beaucoup plus efficace par rapport aux autres méthodes d’ordre inférieur !
La suite
Je pensais que je parlerais d’erreurs (erreur de troncature de la série de Taylor, erreur globale, erreur à chaque pas, etc). Cependant, je pense qu’il y a de nombreuses ressources qui couvrent bien le sujet. Si je trouve une raison de l’expliquer, je le ferai !
Allons à la dynamique des particules !
Des ressources (en anglais)
Mon programme en C qui accompagne ce poste Runge Kutta — 2nd order (with math derivations) Runge Kutta — 4th order (with math derivations) La méthode du point milieu
