Je n’arrête pas de me heurter aux murs en ce qui concerne ma simulation du tissu ! En lisant cet article sur la dynamique basée sur la position, je suis tombé sur le concept de linéarisation locale des fonctions non linéaires. L’auteur a mentionné que :

Le problème, comme toujours, c’est que ce concept m’était inconnu. 🤦‍♂️

Nous avons déjà parlé des fonctions non linéaires lorsque nous avons abordé le sujet des fonctions contraintes dans cet article. Nous poursuivrons cette discussion dans le contexte de simplifier ces fonctions en les linéarisant.

Pourquoi devrais-je m’en soucier ? 🙋 La résolution de fonctions non linéaires peut être une tâche coûteuse, en fonction de sa complexité. Grâce à la linéarisation, il est possible de partitionner des parties linéaires d’une fonction non linéaire pour les résoudre avec des équations linéaires beaucoup plus simples. C’est pour les résoudre plus facilement et à moindre coût en ressources !

Linéarisation avec des plans tangentiels

Pour commencer, définissons rapidement la différence entre une fonction linéaire et une fonction non linéaire :

• Linéaire - une fonction qui fait une ligne droite lorsqu’elle est tracée. Par exemple, examinons ce graphique pour la fonction $y = 2x + 1$ :

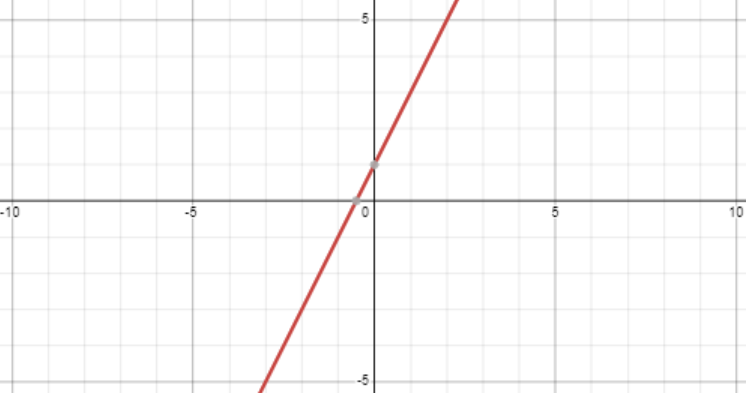
Remarquons que ces fonctions prennent la forme :

Par exemple :

Vous pouvez aussi remarquer que les dérivées partielles sont constantes. Par exemple - une fonction comme $g(x,y) = ax + by + c$ aura des dérivées partielles constantes :

• Non linéaire - il s’agit des fonctions qui ne prennent pas les lignes droites lorsqu’elles sont tracées. Voici la fonction non linéaire $y = x^2 - 1$ :

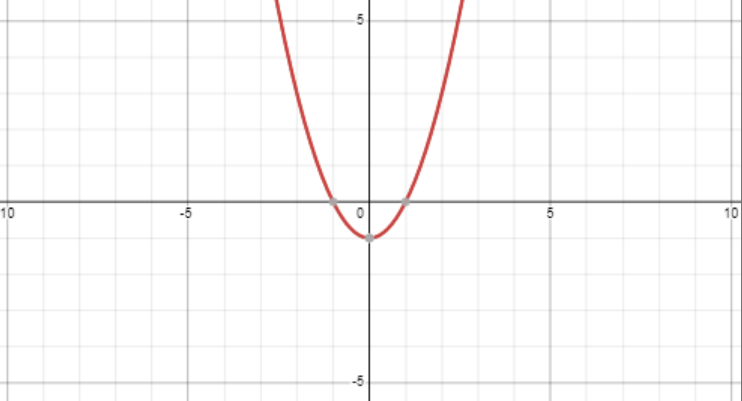
Contrairement aux fonctions linéaires, les dérivées partielles d’une fonction non linéaire ne sont pas entièrement constantes. Voici les dérivées partielles d’une fonction $g(x,y) = x^2 + y^2 + 1$ :

La linéarisation d’une fonction non linéaire peut être résumée en disant que nous aimerions trouver un plan tangent à un point sur un graphique d’une fonction non linéaire. Cette fonction plane sert de fonction linéaire en ce point donné.

Pour clarifier, voici le graphique pour la fonction non linéaire $f(x,y) = x^2+ y^2$ (bleu) et un plan tangent représenté par la fonction $g(x,y)=2(x-1) + 2(y-1) + 2$ (violet) :

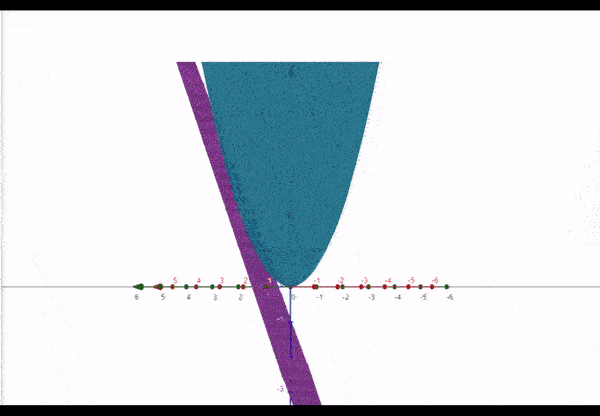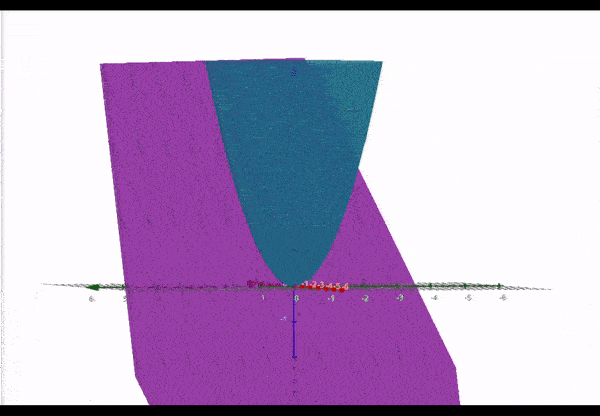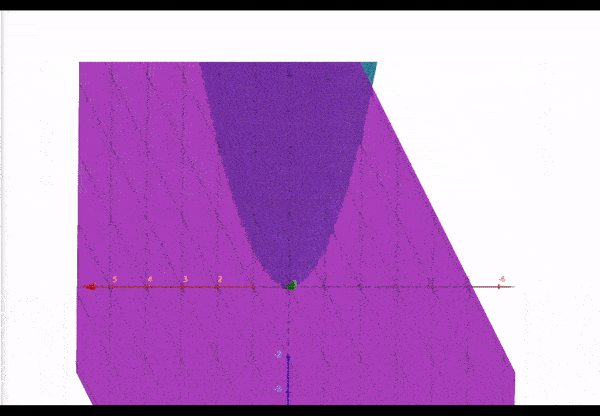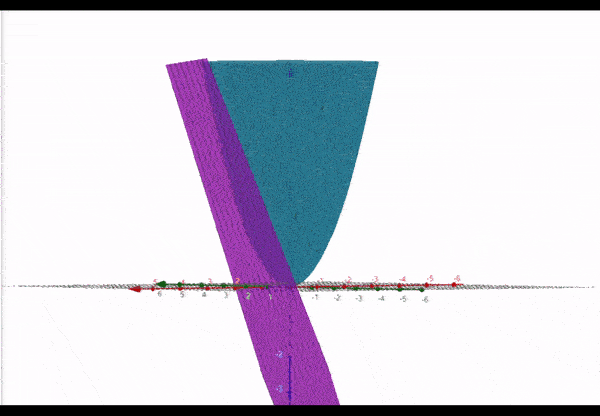
Au point $(1, 1)$, les deux fonctions se croisent. Nous pouvons dire qu’au point $(1,1)$ la fonction est linéarisée comme $g(x,y)$.

Cependant, cette linéarisation empirera au fur et à mesure que nous nous éloignons du point $(1,1)$. C’est pour cela que nous devrions dire que la fonction $f(x,y)$ est linéarisé localement au point $(1, 1)$.

Vu que nous sommes désormais plus familiers avec le concept de linéarisation, nous pouvons l’examiner plus en détail. Rappelez-vous que notre objectif est de comprendre cette équation :

Le plan tangent

Dans la section dernière, j’ai utilisé une fonction $g(x,y)$ pour décrire un plan. Cependant, il semble un peu trop magique. 🪄

Comment trouver l’équation d’un plan ? Pour commencer, voici l’équation d’un plan dans son intégralité :

En utilisant un vecteur normal et deux points qui se trouvent sur le plan, il est possible de trouver son équation.

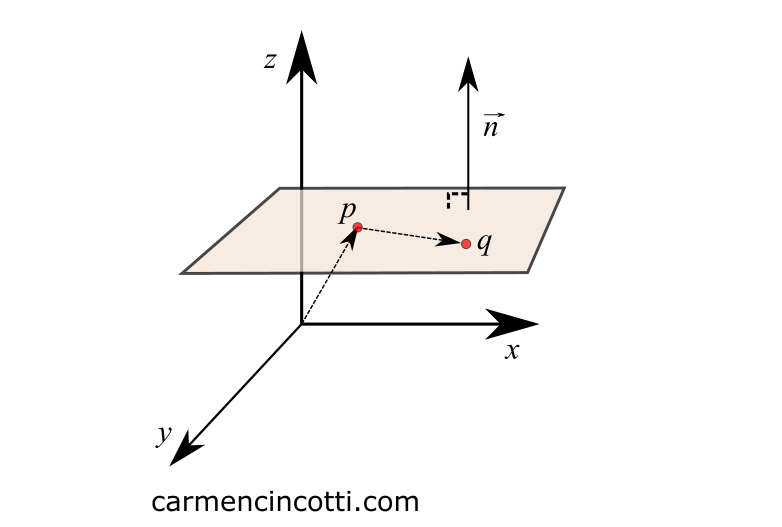
où $\vec{n} = (a,b,c)$ et $\vec{pq} = (x_q - x_p, y_q - y_p, z_q - z_p)$. $\vec{pq}$ se trouve entièrement sur le plan.

Nous savons que le produit scalaire entre deux vecteurs perpendiculaires est 0. Cela nous laisse avec la forme suivante $\vec{n} \cdot \vec{pq} = 0$.

Enfin, je vais réécrire cette équation sous une forme où le vecteur $\mathbf{x_0}$ est la position d’intersection du plan et d’une fonction non linéaire :

Gardez cette équation à l’esprit parce que nous la verrons dans la prochaine partie !

Linéarisation locale

Vu que nous connaissons l’équation d’un plan - nous pouvons ajouter à cette connaissance. Supposons que nous voulions approximer la fonction précédente $f(x,y) = x^2+ y^2$ en trouvant son approximation linéaire locale.

Pour ce faire, nous voulons trouver une fonction d’un plan qui est tangente à la fonction au point $(x,y,z)$.

Les entrées de la fonction $f(x,y)$ nous donnent la valeur $z$. Nous pouvons donc dire que le plan et la fonction $f(x,y)$ se croisent au point $(x, y, f(x,y))$.

Ensuite, nous pouvons réécrire l’équation d’un plan $a(x - x_0) + b(y - y_0) + c(z - z_0) = 0$ pour se débarrasser de la variable $c$ et pour séparer $z$ :

Comment allons-nous continuer ? 🤔

Une caractéristique importante d’une courbe tangentielle

Eh bien, la chose la plus importante à retenir lorsqu’on parle des courbes tangentielles est qu’une courbe et sa contrepartie tangentielle doivent avoir la même pente au point d’intersection !

Sinon, elles ne peuvent pas être tangentielles. Regardez ces deux graphiques 2D :

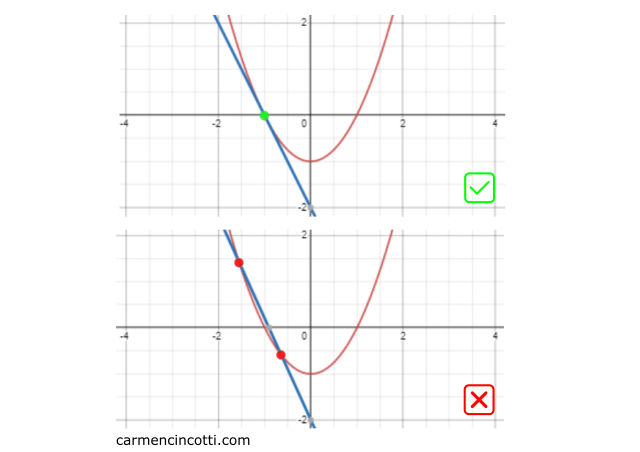
• Le graphique du haut montre deux courbes qui se croisent à peine à un seul point - $(-1,0)$, ce qui signifie que la courbe bleue est tangente à la courbe rouge. ✅

• Le graphique du bas a deux intersections ce qui signifie que la ligne bleue n’est pas tangente à la courbe rouge. ⛔

Vous vous posez peut-être la question :

Comment trouver la pente de $f(x,y)$ ? 🤔

La pente est le gradient $\nabla f(x,y)$ ! Rappelons que le gradient se compose des dérivées partielles d’une fonction de plusieurs variables.

En utilisant les dérivées partielles de $f(x,y)$ - $f_x$ et $f_y$ - nous pouvons supposer que :

Enfin, nous réécrivons cette équation en sachant que les deux points se croisent au point $(x, y, f(x,y))$ et en posant $L_f(x,y) = f(x,y) = z$ pour être clair que la fonction $L_f(x,y)$ est l’approximation linéaire locale de $f(x,y)$ :

Réécriture de la fonction

Rappelons que la fonction linéaire que nous avons utilisée est la suivante :

Nous pouvons réécrire notre fonction $L_f(x,y)$ sous cette forme en utilisant $\mathbf{x} = (x, y)$ et $\mathbf{x}_0 = (x_0, y_0)$ :

…qui est la même forme de la fonction contrainte de l’introduction, mais où $\mathbf{x}_0 = x$ et $\mathbf{x} = x+\Delta x$ :

Des ressources (en français et anglais)

• Linear and Non-Linear Functions
• Equations of Planes - Paul’s Online Notes
• Scalar Equation of a Plane - J. Garvin
• Tangent Planes and Linear Approximations - Paul’s Online Notes
• What are the benefits of linearization? - Stack Exchange