Créons un système de particules - Partie 2

Nous créons un système de particules à partir de zéro en JavaScript en utilisant HTML Canvas et des ressorts.

Keywords: les force newtoniennes, des méthodes numériques, maths, les simulations physiques

By Carmen Cincotti

March 28, 2022

Le ressort
- La loi de Hooke
- La force entre deux particules
Le code en JavaScript
Le résultat
La suite
Des ressources (en anglais et français)

La semaine dernière, je vous ai promis de continuer mon travail sur des systèmes de particules en implémentant l’exemple qui se trouve dans la dynamique du système de particules sous ‘User Interaction’.

Pour rappel, cette ressource nous demande de fabriquer un système de particules afin de simuler un système masse-ressort. La semaine dernière, j’ai développé la base du projet avec un solveur qui peut résoudre la position d’une particule en :

sommant les forces extérieures agissant sur chacune,
trouvant l’accélération causée par ces forces avec $a = \frac{\sum F}{m}$
utilisant la méthode d’Euler afin de résoudre la vitesse et enfin la position de la particule.

À la fin de ce travail, notre système pouvait seulement simuler l’effet de la force de gravité. Cette semaine, je vous presenterais des ressorts. On va commencer par étudier la loi de Hooke qui nous fera comprendre comment calculer les forces entre deux particules lorsqu’on met un ressort entre elles. Je vais aussi terminer ce prototype avec une interface utilisateur terne, mais charmante quand même, qui nous permettra d’interagir avec et de configurer un système de particules.

Voici le projet terminé

Le ressort

Le ressort sera la vedette de notre projet cette semaine. Avant de voir le code, il faut comprendre la loi de Hooke et comment l’utiliser pour calculer les force entre deux particules.

La loi de Hooke

La loi de Hooke est décrit par Wikipédia comme suit :

En physique, la loi de Hooke modélise le comportement des solides élastiques soumis à des contraintes. Elle stipule que la déformation élastique est une fonction linéaire des contraintes. Sous sa forme la plus simple, elle relie l’allongement (d’un ressort, par exemple) à la force appliquée.

où l’équation de la loi de Hooke s’écrit donc :

F_r = -k_s \Delta l

où F_r est la force de rappel du ressort, k_s est le coefficient de raideur du ressort, et Δl est la variation de longueur du ressort qui est la différence entre sa longueur lorsque le ressort est tiré ou comprimé par une force (représentée par la variable l_f), et sa longueur au repos r :

\Delta l = l_f - r

Pour être sûr de bien comprendre, regardons un exemple. Imaginons que l’on tire sur un ressort de manière à ce qu’il s’allonge d’une longueur arbitraire Δl :

A spring with arbitrary deformation

Le ressort est tiré par la force du poids de la balle. Le changement de longueur Δl peut être mesuré. Par exemple, si l’on mesure Δl égal à $1m$ et k_s égal à 0,5 $\frac{N}{m}$ , on calculerait la force de rappel du ressort en utilisant la loi de Hooke comme suit :

F_r = -(0,5 \frac{N}{m}) * 1m\\ F_r = -0,5N\\

où F_r est négative parce que la force de rappel du ressort veut agir contrairement à la force du poids de la balle et est donc dans le sens opposé à la déformation du ressort. Cela est le cas parce qu’une force n’est pas une valeur scalaire - c’est un vecteur et des vecteurs ont aussi une direction. La force de rappel du ressort agit dans le sens inverse des forces appliquées qui cause la déformation du ressort afin de le rendre à la longueur du ressort au repos !

La force entre deux particules

Heureusement, dans la ressource que je cite souvent, elle nous donne une équation que l’on utilise pour résoudre la force de ressort entre deux particules. On l’écrit :

F_a = \left[k_s(|l| - r) + k_d \frac{\dot l \cdot l}{|l|} \right]\frac{l}{|l|}, F_b = -F_a

Examinons de plus près cette équation. F_a est comme la force de rappel, mais entre deux particules, c’est la force qui tire la particule vers l’autre jusqu’à ce que la distance entre les deux est égale à la longueur du ressort au repos, r. C’est pour cela que $F_b = -F_a$ parce que la force qui tire la particule A vers particule B est égale à la force négative qui tire la particule B vers la particule A et elles se rapprochent au même temps !

Comme je l’ai dit, la longueur du ressort au repos est la variable r. Nous pouvons voir notre première équation :

F_r = -k_s \Delta l

où $\Delta l = |l| - r$ où $|l|$ est l’amplitude de la distance l, entre deux particules. Cette distance entre deux particules est un vecteur où elle peut être trouvée en soustrayant la position de l’une des particules de l’autre : $l = d_b - d_a$ .

Par ailleurs,

F_d = k_d \frac{\dot l \cdot l}{|l|}

est la force d’amortissement du ressort. Cette force amortie est proportionnelle à la vitesse de la déformation du ressort. Sans cela, le système oscillerait pour toujours, car la force de rappel du ressort est une force conservatrice, par rapport à la force d’amortissement qui est non conservatrice. Autrement dit, notre système perdra de l’énergie avec le temps en raison de la force d’amortissement et pourra donc se rapprocher à l’équilibre.

En plus, $\dot l$ est la dérivée de $l$ , qui est donc égale à la différence entre la vitesse de nos particules $\dot l = v_a - v_b$

Pour autant, l’expression $\left[k_s(|l| - r) + k_d \frac{\dot l \cdot l}{|l|} \right]$ résoudra seulement l’amplitude de la force. Ce sera donc juste une valeur scalaire. Il faut donc aussi inclure la direction de la force dans le calcul. Pour ce faire, on multiplie cette amplitude par la direction : $\frac{l}{|l|}$ , qui est la direction normalisée de la force.

À chaque tour de la boucle contrôlée par requestAnimationFrame, ces calculs seront résolus par notre solveur (la méthode d’Euler). Voyons comment je l’ai codé !

Le code en JavaScript

Le code se trouve là

J’ai changé beaucoup de code au cours de cette semaine par rapport au code de la semaine dernière. Je vous laisse scruter tout cela. Je vais revoir le code important pour expliquer uniquement comment simuler la physique mise en œuvre.

Rappelons que l’ensemble du processus de calcul de la position suivante de chaque particule se résume comme suit :

    loop {
        for particule dans le système {
            - avancer d'un pas de temps en avance (deltaTs)
            - accumulez les forces qui agissent sur chaque particule
            - calculez l'accélération de la force sommée (F / m)
            - utilisez une méthode numérique (un solveur) pour résoudre la prochaine position d'une particule
            - mettez à jour le Canvas (redessinez le)
        }
    }

Après avoir initialisé notre système dans le fichier index.html, on commence la simulation de notre système. Voici notre nouvelle version de la fonction run :

// Calculate new positions, then draw frame
const run = currentElapsedTs => {
  clearCanvas(ctx)

  // Store deltaTs, as that acts as our step time
  deltaTs = (currentElapsedTs - lastElapsedTs) / 100
  lastElapsedTs = currentElapsedTs

  // Solve the system, then draw it.
  particleSystem.solve(deltaTs)
  particleSystem.draw(ctx)

  if (drawCb) {
    drawCb()
  }
  // Loop back
  requestAnimationFrame(run)
}
requestAnimationFrame(run)

Juste comme avant, on appelle requestAnimationFrame afin de notifier au navigateur que nous aimerions exécuter une animation (encore une fois, revoie le post de la semaine dernière pour une explication plus complète).

Ensuite, nous arrivons à la méthode de classe la plus importante, solve, qui est responsable de la mise à jour des positions de chaque particule dans le système :

 /**
   * Solve the particle system, which updates all the particles's position
   * @param {number} deltaTs
   */
  solve(deltaTs) {
    ...
    this.forces.forEach((f) => {
      f.applyTo(this);
    });

    this.particles.forEach((p) => {
      EulerStep(p, deltaTs);
    });
    ...
  }

Cette fois-ci, on introduit une nouvelle force que l’on doit résoudre, ce que je nomme dans le code comme SpringForce (ForceDuRessort).

/**
 * A spring force between two particles
 */
class SpringForce extends Force {
  constructor(spring) {
    super()
    this.spring = spring
  }

  applyTo(_pSystem) {
    const { p1, p2, ks, kd, r } = this.spring
    const calculateForce = () => {
      // Vector pointing from particle 2 to particle 1
      const l = p1.position.clone().sub(p2.position)

      // distance between particles
      const distance = l.magnitude()

      // Find the time derivative of l (or p1.velocity - p2.velocity)
      const l_prime = p1.velocity.clone().sub(p2.velocity)

      // Calculate spring force magnitude ks * (|l| - r)
      // The spring force magnitude is proportional to the actual length and resting length
      const springForceMagnitude = ks * (distance - r)

      // Calculate damping force magnitude kd * ((l_prime * l) / l_magnitude)
      const l_dot = l_prime.dot(l)
      const dampingForceMagnitude = kd * (l_dot / distance)

      // Calculate final force vector
      // fa = − [springForceMag + dampingForceMag] * (l / |l|)
      const direction = l.clone().normalize()
      return direction.multiplyScalar(
        -1 * (springForceMagnitude + dampingForceMagnitude)
      )
    }
    const f1 = calculateForce()
    p1.applyForce(f1)

    const f2 = f1.clone().multiplyScalar(-1)
    p2.applyForce(f2)
  }
}

Dans la méthode SpringForce.applyForce, on fait le calcul de la force du ressort entre deux particules. Vous pouvez voir qu’il s’agit exactement d’une implémentation de notre équation ci-dessus :

F_a = \left[k_s(|l| - r) + k_d \frac{\dot l \cdot l}{|l|} \right]\frac{l}{|l|}, F_b = -F_a

Cette force calculée va s’ajouter à l’accumulateur de force sur chaque particule, ce qui va influencer le calcul de sa position par le solveur !

Enfin, on passe l’accumulateur de force à la fonction EulerStep afin de calculer la position de chaque particule dans le système.

/**
 * Given a particle and a time step, this function updates the given particles
 * position and velocity properties determined by taking a EulerStep
 *
 * @param {Particle} p
 * @param {number} deltaTs
 */
function EulerStep(p, deltaTs) {
  // Calculate acceleration step
  const accelerationStep = p.f
    .clone()
    .divideScalar(p.mass)
    .multiplyScalar(deltaTs) // aΔt = F / m

  p.velocity.add(accelerationStep) // vn = vo +  a*Δt
  p.velocity.multiplyScalar(p.damping)

  // Calculate velocity step
  const velocityStep = p.velocity.clone().multiplyScalar(deltaTs) // vn*Δt
  p.position.add(velocityStep) // xn = x0 + vn*Δt
}

Le résultat

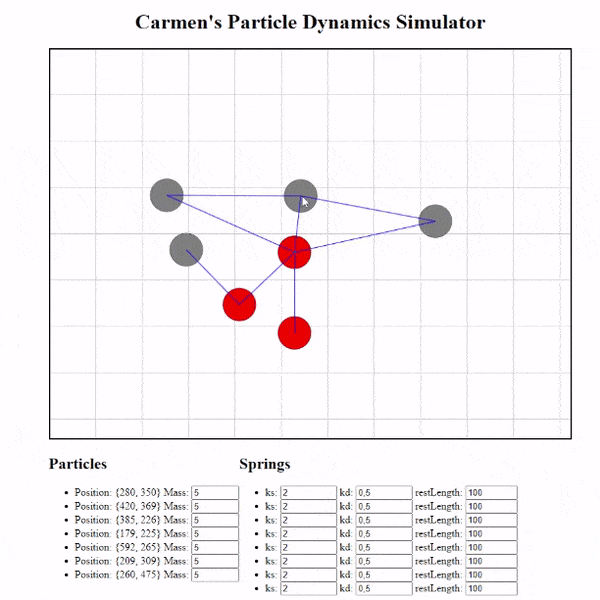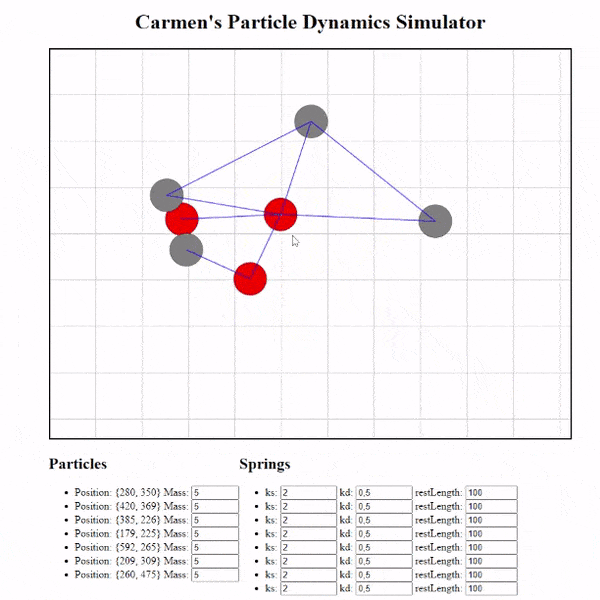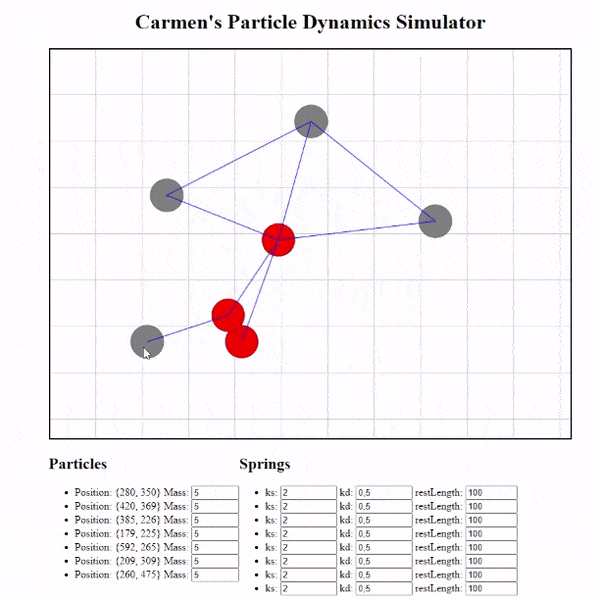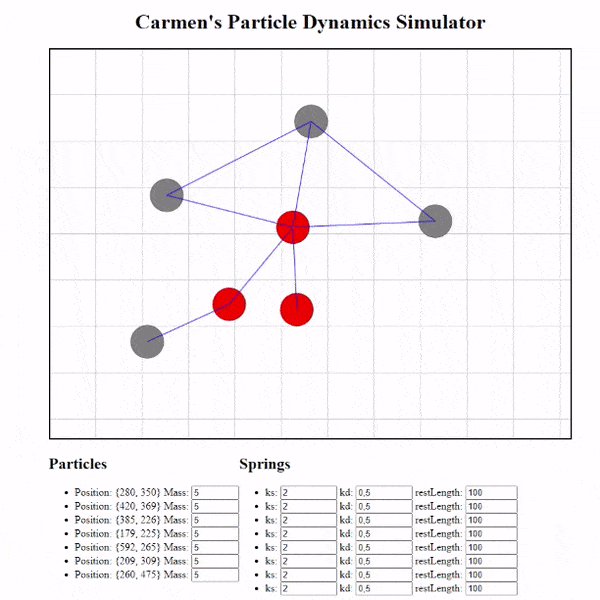
Code result

Voici le projet terminé

J’ai aussi ajouté de nombreux gestionnaires pour créer des particules, créer des ressorts entre les particules et la possibilité de modifier les propriétés de nos ressorts !

La suite

On continue à lire Pixar Physics Simulation Animation Course. Il me semble que je lirai la partie sur des méthodes implicites.

Carmen's Graphics Blog