En lisant l’article sur la dynamique basée sur la position, je me suis rendu compte qu’il y a pas mal de concepts mathématiques que je ne comprends pas très bien. 😕

Par exemple, dans le contexte des contraintes, il existe des concepts tels que le gradient d’une fonction. En plus, quand on parle de l’optimisation d’une fonction qui est contrainte, on parle souvent du multiplicateur de Lagrange et aussi du lagrangien.

Lors de cet article, mon objectif est de démystifier ces concepts.

Le gradient

Avant de découvrir le pourquoi du gradient, je propose que nous regardions d’abord comment résoudre le gradient d’une fonction de plusieurs variables telle que $f(x,y,z)$. Le gradient est un vecteur constitué des dérivées partielles de la fonction définie, $f$ :

où $\nabla$ est appelé nabla. Il est parfois appelé “del”. Il désigne l’opérateur différentiel vectoriel.

Prenons un exemple. J’ai une fonction définie comme $f(x,y) = 5x + 3xy$. Tout d’abord, on doit trouver les dérivées partielles par rapport aux variables $x$ et $y$ comme suit :

Cela nous donne un gradient :

C’était assez facile à résoudre ! Néanmoins, l’importance du gradient reste un mystère que nous allons découvrir dans la section suivante. 🕵️‍♂️

La signification du gradient

Imaginons que nous sommes au pied d’une montagne et que nous voulons la grimper le plus rapidement possible. On voit que la bonne piste est de la gravir dans le sens de la flèche :

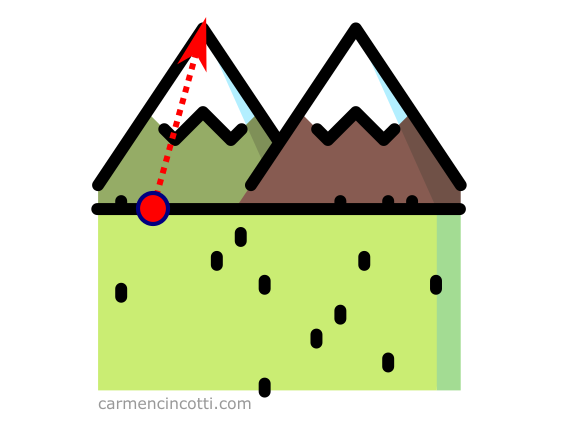
Cette flèche représente le gradient parce que c’est l’ascension la plus rapide de la montagne.

En termes plus précis, le vecteur gradient est la direction et le taux d’augmentation le plus rapide d’une fonction $f$ à un point donné. Ce concept est le point le plus important à retenir sur le gradient. 💡

Imaginons que nous créons une carte thermique pour une fonction $f$ dans un espace arbitraire. Ensuite, nous trouvons le gradient à différentes entrées de $f$ telles que $(x_0, y_0, ...), (x_1, y_1, ...), ... ( x_n, y_n, ... )$. Si nous représentons le gradient à chacun de ces points sous forme de flèches, nous pourrions voir l’image suivante :

By Vivekj78 - Own work, CC BY-SA 3.0, Link

Nous pouvons voir que le gradient $\nabla{f}(x, y,...)$ nous indique la direction pour maximiser la valeur de $f$ à chaque entrée donné.

En plus, la magnitude, $|| \nabla{f}(x_0, y_0,...) ||$, nous donne la pente de cette ascension.

Le gradient et les lignes de contour

Regardons ce graphique pour l’équation $f(x,y) = x^2 + y ^2$ :

Si nous l’écrasons d’un espace tridimensionnel à un espace bidimensionnel, nous verrons ces cercles qui représentent l’espace d’entrée, x et y, tandis que la troisième valeur z (qui représente la sortie de la fonction $f(x,y)$) est désignée par les textes 1, 2, 3, 4, 7 :

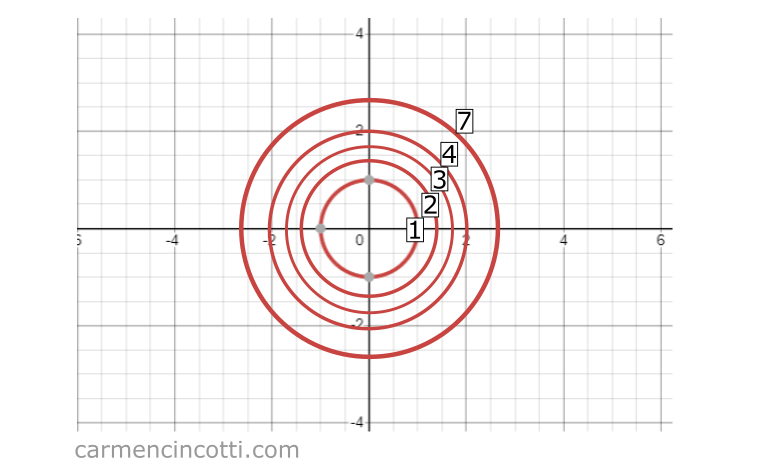
Une caractéristique importante des graphiques de contour, c’est qu’ils peuvent nous aider à trouver les pics et les vallées d’une fonction.

Quand les lignes (au bas du graphique ci-dessus) sont éloignées les unes des autres, la pente n’est pas raide. À l’inverse, si les lignes sont proches les unes des autres, la pente est raide.

Cela est un important point quand nous examinons la relation entre le gradient et un graphique de contour.

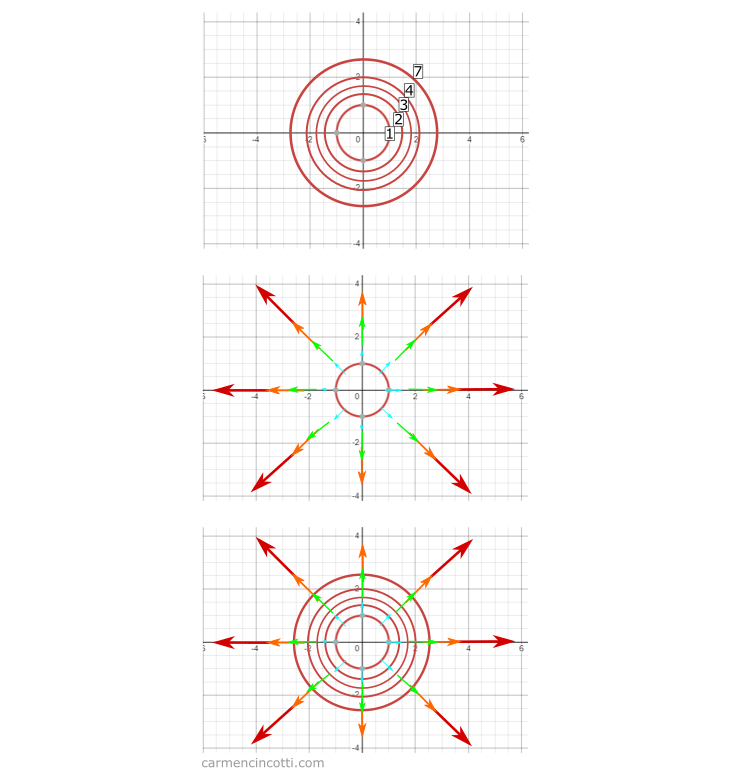
Comme vous pouvez le voir, chaque vecteur de gradient est perpendiculaire à la ligne de contour qu’il touche. Ce comportement est observé parce que la piste la plus courte entre des lignes est une ligne perpendiculaire les unes aux autres.

Cela a du sens, parce qu’on a déjà défini le gradient comme la direction et le taux d’augmentation le plus rapide d’une fonction $f$.

Application du gradient - problème d’optimisation sous contraintes

L’objectif d’un problème d’optimisation sous contraintes est de maximiser ou minimiser une fonction de plusieurs variables $f(x,y,z,...)$.

Une fonction contrainte prend la forme $g(x,y,z,...) = c$.

Si je prends une fonction de plusieurs variables $f(x,y)$ et une fonction contrainte $g(x,y)$ telles que :

Notre but est de trouver le point où $f(x,y)$ et $g(x,y)$ sont tangents quand $c = g(x,y) = 2$ comme suit :

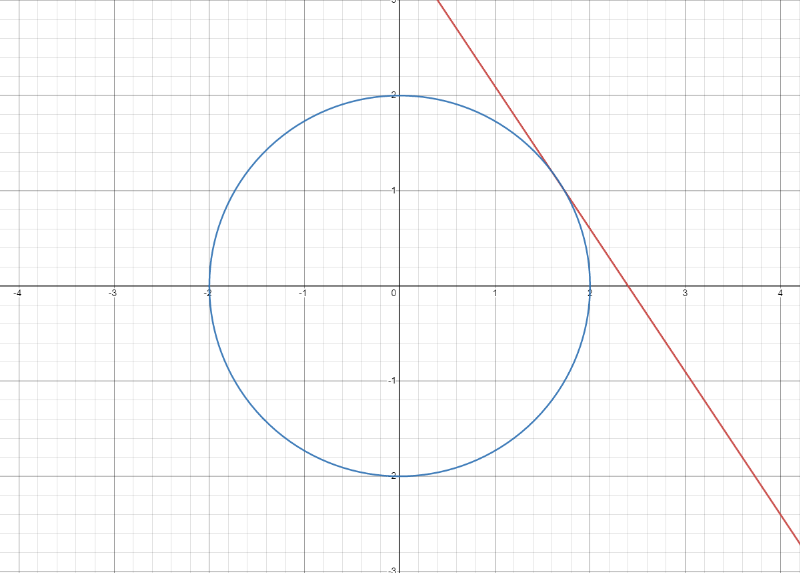
Pour ce faire, nous pouvons trouver les valeurs maximales de $x$ et $y$ en utilisant notre connaissance du gradient.

Nous savons déjà le fait que le gradient se pointe dans le sens perpendiculaire aux courbes de contour.

Cependant, les magnitudes de $\nabla f(x,y)$ et de $\nabla g(x,y)$ ne sont pas pareils. Il faut donc corriger cette différence avec un scalaire, $\lambda$ qui s’appelle le multiplicateur de Lagrange :

Nous savons déjà pour trouver les valeurs $\nabla f(x,y)$ et $\nabla g(x,y)$, il faut prendre la dérivée partielle de chacune par rapport à x et y :

Nous pouvons résoudre les valeurs $\lambda, x, y$ en résolvant le système d’équations suivant :

Ce qui nous donne les équations :

En résolvant pour $x$ et $y$ :

Supposons que nous voulions maximiser $f(x,y)$. On testerait ces points comme entrées de la fonction. La bonne réponse serait $(1.66, 1.11)$

Le lagrangien

Nous pouvons reformuler ces fonctions en les écrivant sous la forme :

Cette fonction s’appelle le lagrangien.

Pourquoi devrais-je écrire encore une autre nouvelle forme de la fonction ? 🤔

En pratique, un ordinateur résout souvent ces problèmes d’optimisation. Cette forme les encapsuler mieux. Sans ordinateur, il serait probablement plus facile de séparer les fonctions comme nous l’avons déjà fait.

Pour l’instant, je vous laisse faire vos propres recherches à ce sujet ! Voici un point de départ.

Des ressources (en français et anglais)

• Contour maps - Khan Academy
• The gradient - Khan Academy
• Lagrange multipliers, introduction - Khan Academy
• Lagrange multipliers, examples - Khan Academy