La jacobienne contre l'hessienne contre le gradient

Quelles sont les différences entre la jacobienne, l'hessienne et le gradient ? Tous les trois ont des liens avec le calcul à plusieurs variables, plongeons-y et jetons un coup d'œil !

Keywords: calcul à plusieurs variables, intelligence artificielle, optimisation, physique

By Carmen Cincotti

August 15, 2022

Le Gradient
- Une fonction à valeur scalaire
- Comment calculer le Gradient
La hessienne
- Le déterminant de Hesse
La jacobienne
- Le déterminant de la matrice jacobienne
Des ressources (en français et anglais)

En étudiant le calcul à plusieurs variables, on rencontre souvent l’utilisation de matrices pour représenter des notions différentes. On croise souvent la jacobienne, l’hessienne et le Gradient.

Jacobienne vs hessienne

Ces notions sont proches les unes des autres, en vertu d’être des matrices ayant à voir avec des dérivées de fonctions. Cependant, chaque matrice a sa propre dérivation et sa propre signification.

Quelle est la différence entre la jacobienne, l’hessienne et le Gradient 🤔 ? Nous allons la découvrir ensemble lors de cet article. Au cours de ce voyage mathématique, on étudiera également les concepts de la différence entre des fonctions à valeurs vectorielles (vector valued functions) et des fonctions à valeurs scalaires (scalar valued functions).

Le Gradient

On commence par le gradient dont nous avons déjà parlé il y a quelques semaines. Le gradient est un vecteur composé des dérivées partielles d’une fonction à valeur scalaire, $f$ :

\nabla{f}(x, y, z) = \begin{bmatrix} \frac{\partial f}{\partial x} \\[6pt] \frac{\partial f}{\partial y} \\[6pt] \frac{\partial f}{\partial z} \\ \end{bmatrix}

où $\nabla$ s’appelle nabla. Il s’appelle parfois “del”. Il désigne l’opérateur différentiel vectoriel.

Rappelons que le gradient mesure la direction et le taux d’augmentation le plus rapide d’une fonction $f$ à un point donné.

Imaginons que nous sommes au pied d’une montagne et que nous voulons la grimper le plus rapidement possible. On voit que la bonne piste est de la gravir dans le sens de la flèche :

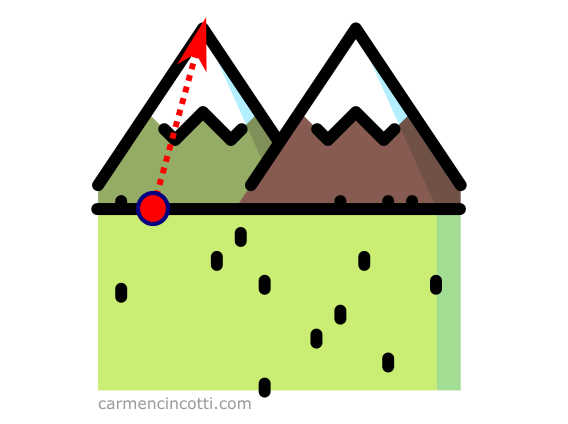
Person climbing a mountain

Cette flèche représente le gradient parce que c’est l’ascension la plus rapide de la montagne.

Une fonction à valeur scalaire

Une fonction à valeur scalaire est une fonction (à plusieurs variables / de dimensions $n$ ) qui renvoie une valeur scalaire :

f: \mathbb{R}^n \rightarrow \mathbb{R}

Par exemple, si nous évaluons $f(x,y) = x + y$ au point (2,1), on reçoit le scalaire, 3 :

f(2,1) = 2 + 1 = 3\\[6pt]

Comment calculer le Gradient

Prenons un exemple. J’ai une fonction définie comme $f(x,y) = 5x^2 + 3xy + 3y^3$ . Tout d’abord, on doit trouver les dérivées partielles par rapport aux variables $x$ et $y$ comme suit :

\frac{\partial f}{\partial x} = 10x + 3y \\[6pt] \frac{\partial f}{\partial y} = 3x + 9y^2 \\[6pt]

Cela nous donne un gradient :

\nabla{f} = \begin{bmatrix} 10x + 3y \\[6pt] 3x + 9y^2 \\ \end{bmatrix}

La hessienne

Si l’on suit bien l’explication du gradient, l’hessienne sera également facile à comprendre. C’est la dérivée du gradient d’une fonction à valeur scalaire $f: \mathbb{R}^n \rightarrow \mathbb{R}$ . Par exemple :

\mathbf{H}f(x, y) = \nabla{}^2f(x, y) = \begin{bmatrix} f_{xx} & f_{xy} \\[6pt] f_{yx} & f_{yy} \\[6pt] \end{bmatrix}

En utilisant à nouveau la fonction $f(x,y) = 5x^2 + 3xy + 3y^3$ , on verra une matrice hessienne comme suit :

\mathbf{H}f(x, y) = \nabla{}^2f(x, y) = \begin{bmatrix} 10 & 3 \\[6pt] 3 & 18y \\[6pt] \end{bmatrix}

Quelques applications de la matrice hessienne sont les suivantes :

Les approximations quadratiques d’une fonction à plusieurs variables. Il s’agit d’une approximation plus proche de la fonction que l’approximation linéaire locale dont nous avons déjà parlé il y a plusieurs semaines.
Le test de la seconde dérivée partielle - il est utilisé pour trouver les points-selles (point col), les maxima et les minima d’une fonction.

Le déterminant de Hesse

Le déterminant de Hesse joue un rôle dans la recherche des maxima/minima locaux d’une fonction à plusieurs variables. Nous verrons ce qu’il est un déterminant dans un article ultérieur. Pour l’instant, je vais juste expliquer comment le calculer. Je vous présente à nouveau la matrice hessienne que nous avons déjà calculée dans la partie dernière :

\mathbf{H}f(x, y) = \nabla{}^2f(x, y) = \begin{bmatrix} 10 & 3 \\[6pt] 3 & 18y \\[6pt] \end{bmatrix}

Afin de trouver le déterminant, nous devons suivre le framework ci-dessous :

\det\begin{pmatrix}\begin{bmatrix} a & b \\[6pt] c & d \\[6pt] \end{bmatrix}\end{pmatrix} = ad-bc

Donc,

\det\begin{pmatrix}\begin{bmatrix} 10 & 3 \\[6pt] 3 & 18y \\[6pt] \end{bmatrix}\end{pmatrix} = 180y - 9

La jacobienne

La jacobienne est une matrice qui contient toutes les dérivées partielles du premier ordre d’une fonction à valeurs vectorielles :

f: \mathbb{R}^n \rightarrow \mathbb{R}^n

La forme de la jacobienne d’une fonction à valeur vectorielle $h(f(x,y), g(x, y))$ est donc la suivante :

\mathbf{J}h(f(x,y), g(x,y)) = \begin{bmatrix} f_x & f_y \\[6pt] g_x & g_y \\[6pt] \end{bmatrix}

Par exemple - si nous avons une fonction à valeurs vectorielles comme :

f(x,y): \begin{bmatrix} sin(x) + y \\[6pt] x + cos(y) \end{bmatrix}

La matrice jacobienne serait :

J(f) = \begin{bmatrix} cos(x) & 1 \\[6pt] 1 & -sin(y) \end{bmatrix}

En utilisant le jacobien, nous pouvons linéariser localement une fonction à valeur vectorielle en un point spécifique.

Les fonctions linéaires sont suffisamment simples pour que nous puissions bien les comprendre (en utilisant l’algèbre linéaire), et souvent comprendre l’approximation linéaire locale de $f(x,y) nous permet de tirer des conclusions sur$ f $$ lui-même.

Pour en savoir plus sur le calcul, voici une vidéo qui m’a beaucoup aidé :

Le déterminant de la matrice jacobienne

Nous pouvons utiliser la matrice jacobienne d’une transformation à valeur vectorielle pour trouver son déterminant. Pour ce faire avec une transformation de $f: \mathbb{R}^3 \rightarrow \mathbb{R}^3$ , on utilise le framework :

\det\begin{pmatrix}{\begin{bmatrix} a_1 & a_2 & a_3 \\[6pt] b_1 & b_2 & b_3 \\[6pt] c_1 & c_2 & c_3 \\[6pt] \end{bmatrix}}\end{pmatrix} = a_1 \det\begin{pmatrix}\begin{bmatrix} b_2 & b_3 \\[6pt] c_2 & c_3 \\[6pt] \end{bmatrix}\end{pmatrix} - a_2 \det\begin{pmatrix}\begin{bmatrix} b_1 & b_3 \\[6pt] c_1 & c_3 \\[6pt] \end{bmatrix}\end{pmatrix} + a_3 \det\begin{pmatrix}\begin{bmatrix} b_1 & b_2 \\[6pt] c_1 & c_2 \\[6pt] \end{bmatrix}\end{pmatrix}

Prenons cet exemple en utilisant cette matrice jacobienne :

J(f)=\begin{bmatrix} 2xy & x^2 & 0 \\[6pt] 0 & -1 & 1 \\[6pt] 1 & 0 & 1 \end{bmatrix}

Nous pouvons calculer le déterminant comme suit :

\det\begin{pmatrix}\begin{bmatrix} 2xy & x^2 & 0 \\[6pt] 0 & -1 & 1 \\[6pt] 1 & 0 & 1 \end{bmatrix}\end{pmatrix} = 2xy \det\begin{pmatrix}\begin{bmatrix} -1 & 1 \\[6pt] 0 & 1 \\[6pt] \end{bmatrix}\end{pmatrix} - x^2 \det\begin{pmatrix}\begin{bmatrix} 0 & 1 \\[6pt] 1 & 1 \\[6pt] \end{bmatrix}\end{pmatrix} + 0 \det\begin{pmatrix}\begin{bmatrix} 0 & -1 \\[6pt] 1 & 0 \\[6pt] \end{bmatrix}\end{pmatrix}

= 2xy(-1(1) - (1(0))) - x^2(0(1) - 1(1)) + 0(0(0) - (-1(1)))\\[6pt] = 2xy(-1) - x^2(-1) + 0 \\[6pt] = -2xy + x^2

Qu’est-ce que le déterminant signifie ? 🤔 La fonction $-2xy+x^2$ nous donne l’amplitude dans laquelle l’espace se contracte ou s’élargir lors d’une transformation autour d’un point $(x, y, z)$ .

Par exemple, si on l’évalue au point $(1, 0, 2)$ , on verra :

= -2(1)(0) + 1^2 \\[6pt] = 0 + 1 \\[6pt] = 1

Ce qui nous indique que l’espace ne change pas autour de ce point ! Cependant, autour du point $(3, 1, 0)$ , on voit une autre histoire :

= -2(3)(1) + 3^2 \\[6pt] = -6 + 9 \\[6pt] = 3

Ainsi, autour de ce point, l’espace s’étend jusqu’à trois fois sa taille d’origine !

Je recommande cette ressource afin de visualiser les transformations et le déterminant pour chacune !

Carmen's Graphics Blog