La semaine dernière, nous avons parlé des tables de hachage (ou en anglais - hash tables) afin de mieux les comprendre.

L’objectif est d’utiliser éventuellement une table de hachage spatiale (spatial hash table) pour notre simulation de tissu, car nous devrons l’utiliser pour gérer les collisions de particules.

Lors de l’ajout d’éléments à une telle structure, nous devons faire attention aux collisions de hachage. Au cours des prochains articles, nous apprendrons à les gérer au fur et à mesure qu’ils surviennent.

Qu’est-ce que une collision de hachage ?

Une collision de hachage se produit lorsque deux clés (ou plus) sont hachées au même indice du tableau sous-jacent de hachage.

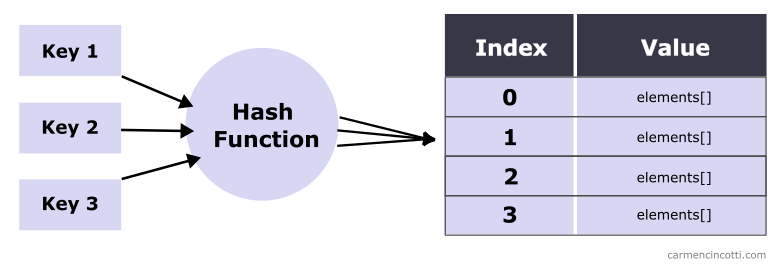
Sans moyens suffisants pour gérer une telle situation, nous aurons des résultats inattendus.

Pourquoi la collision de hachage est-elle un problème ?

Parce que nous allons écraser les données existantes qui sont déjà stockées dans la table de hachage.

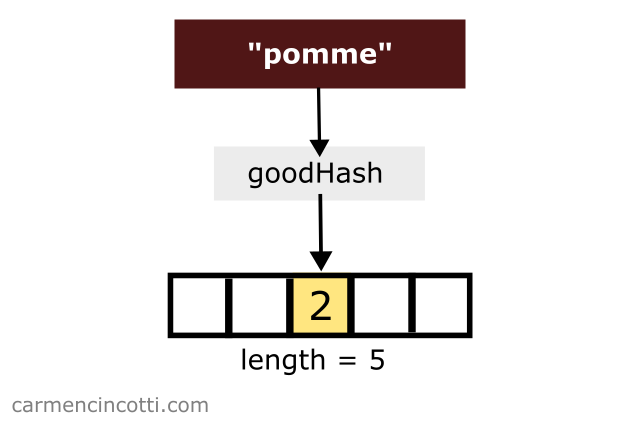
Pour illustrer une telle situation, imaginons que nous voudrions stocker la paire clé-valeur { "pomme": 2 }. Nous avons une fonction de hachage qui hache la clé, pomme, à l’indice de $2$.

Ensuite, nous aimerions stocker{ "pamplemousse": 3} dans notre table de hachage. Par coïncidence, la fonction de hachage hache pamplemousse à l’indice de $2$… mais la valeur de pomme est déjà là !

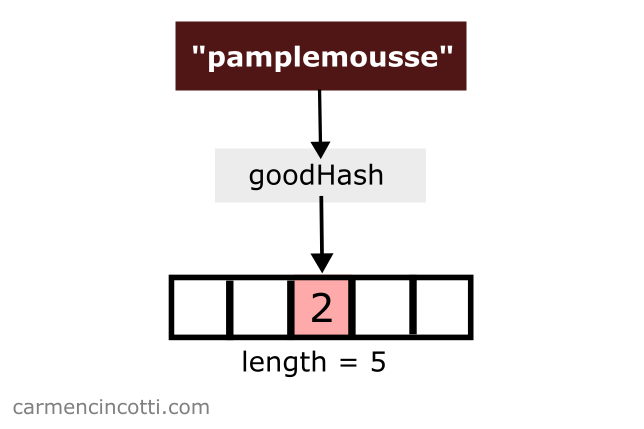
Que pouvons-nous faire pour gérer cette situation ?

Comment gérer une collision de hachage ?

Pour résoudre une collision de hachage, nous avons plusieurs options :

1. Chaînage séparé (Separate Chaining) - une liste chaînée est utilisée à chaque index du tableau pour stocker les données des clés en collision.
2. Adressage ouvert (Open addressing) - En cas de collision, le tableau est parcouru pour trouver un seau ouvert pour stocker les données. Une structure de données supplémentaire n’est pas nécessaire.

La complexité de chaque méthode est mesurée par ce que l’on appelle le facteur de charge de la table de hachage. Nous verrons ce concept dans le prochain article.

Qu’est-ce que le chaînage séparé (separated chaining) ?

Le chaînage séparé est un moyen de résoudre les collisions de hachage dans une table de hachage. Des listes chaînées sont placées à chaque indice du tableau sous-jacent. Chaque paire clé-valeur qui correspond à un certain indice du tableau (après avoir haché la clé) est ajoutée à la liste chaînée.

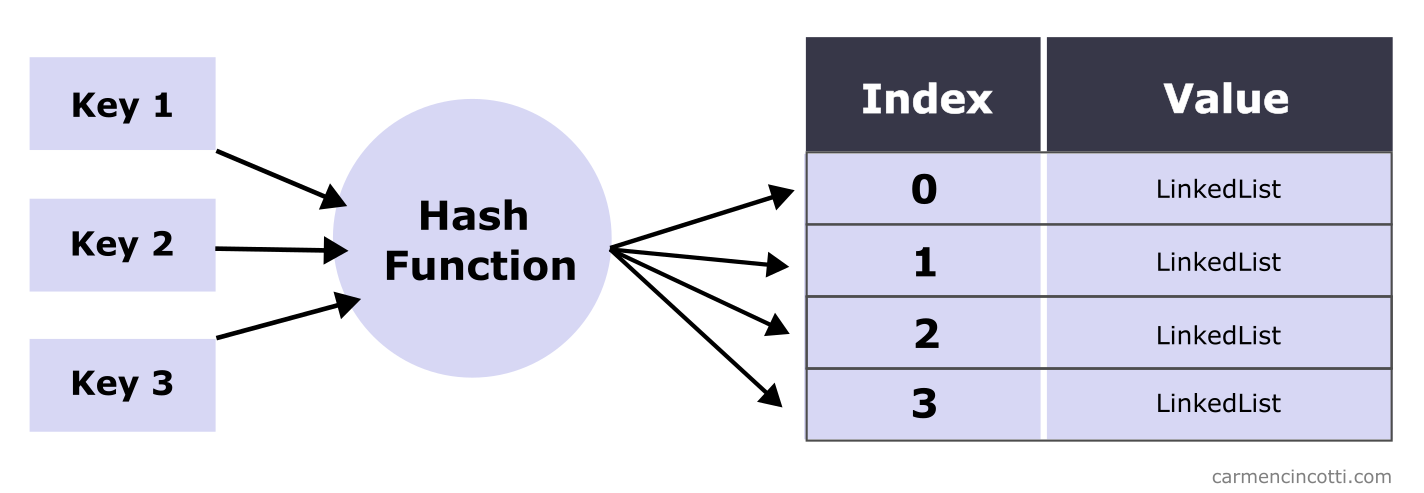
La complexité temporelle pour l’insertion, la recherche et la suppression en moyenne tend ver $O(1)$, étant donné que le tableau sous-jacent est suffisamment grande pour contenir les éléments uniques que nous voulons stocker et que la fonction de hachage distribue uniformément les éléments.

À l’autre extrême, la complexité temporelle de ces opérations peut ressembler à celle d’une liste chaînée si les éléments se regroupent dans un seul seau. Autrement dit, la complexité temporelle se dégrade en $O(n)$ pour l’insertion, la recherche et la suppression.

Chaînage séparé - comment insérer un élément ?

Imaginons qu’il y a une paire clé-valeur { "key": 1 } qui est hachée à l’indice $4$. Je pourrais insérer cette paire en la concaténant à la liste chaînée qui se trouve à cet indice comme suit :

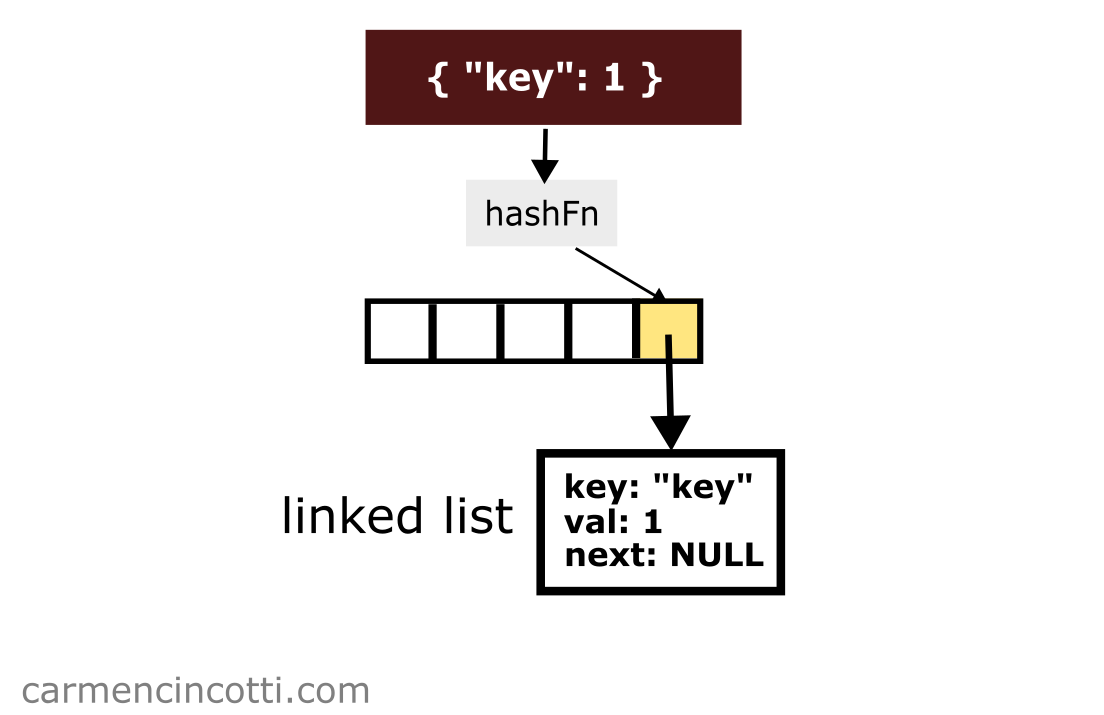
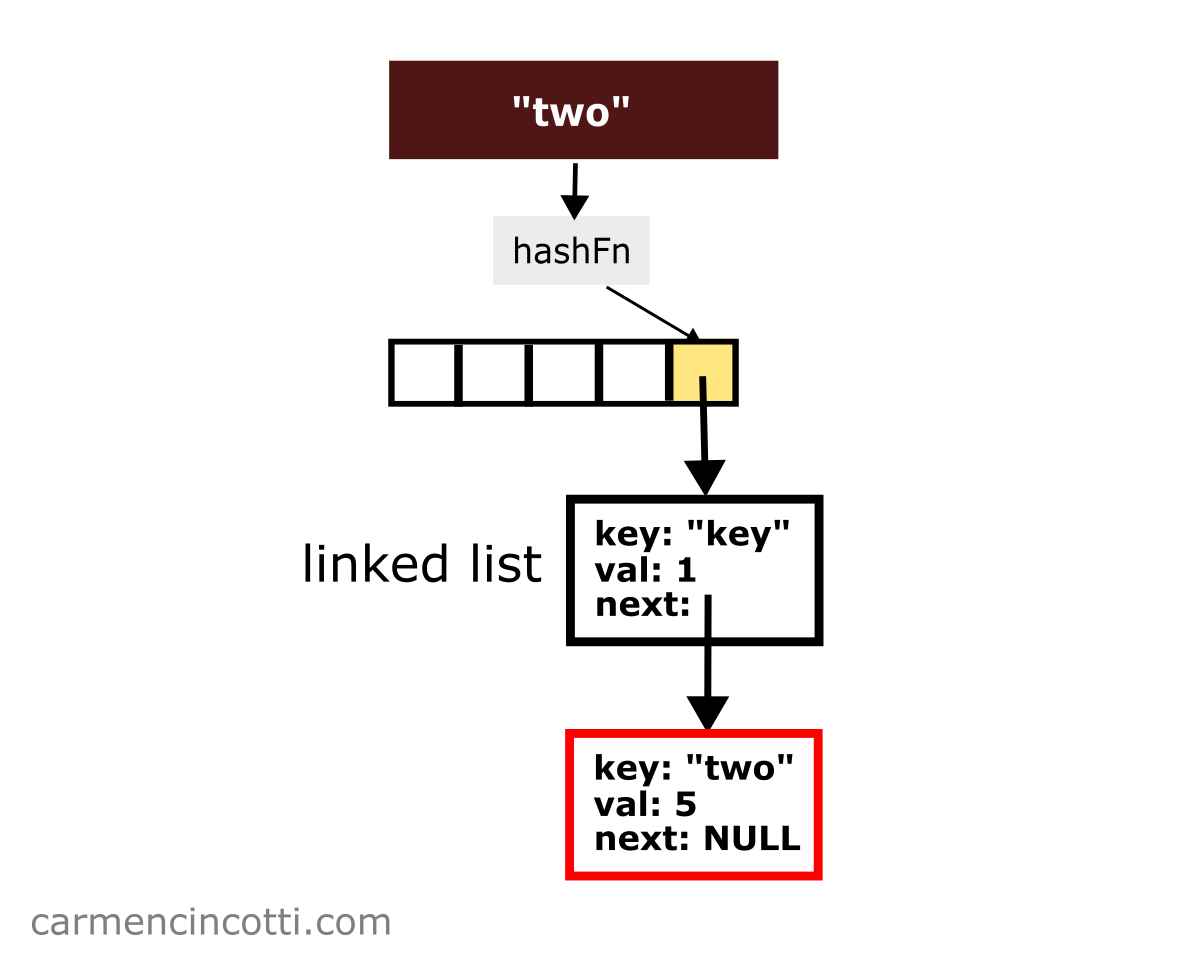
Ensuite, imaginons que je voudrais insérer la paire clé-valeur { "two": 5 } qui est hachée au même indice $4$ :

Il faudrait juste concaténer cette nouvelle paire à la liste chaînée !

Le chaînage séparé - comment rechercher un élément ?

Pour rechercher un élément, nous hachons la clé pour trouver l’indice dans le tableau sous-jacent. Ensuite, on traverse la liste chaînée qui s’y trouve. En utilisant la clé, nous pouvons visiter et comparer chaque nœud de la chaîne jusqu’à ce que nous trouvions une correspondance.

Bien sûr - il y a le cas où rien n’est trouvé. Chaque langue gère ce cas différemment. Peut-être qu’il renverra NULL ou qu’il pourra même générer une erreur.

Le chaînage séparé - comment supprimer un élément ?

Après avoir trouvé le nœud qui correspond à la clé, nous le supprimons en déconnectant le nœud de la liste chaînée.

Quelle est la compléxité temporelle ?

Avec l’aide de cette stratégie pour résoudre les collisions, la complexité temporelle pour rechercher, insérer ou supprimer un élément (en moyenne) est la suivante :

Et dans le scénario du pire des cas, nous verrions ces complexités temporelles :

Un scénario du pire des cas peut être causer par un tableau sous-jacent qui n’est pas assez grand. Une autre cause peut être une fonction de hachage qui crée des regroupements dans un seul seau.

La suite

La semaine prochaine - nous examinerons l’adressage ouvert, le double hachage et le facteur de charge - restez à l’écoute !

Des ressources (en français et anglais)

• Table de hachage - Developpez
• Separate Chaining - Scaler Topics
• Separate Chaining Collision Handling Technique in Hashing - Geeks for Geeks