Qu’est-ce que l’adressage ouvert (open addressing) ?
L’adressage ouvert est une méthode alternative pour résoudre les collisions de hachage. Contrairement au chainage séparé - il n’y a pas de listes chaînées.
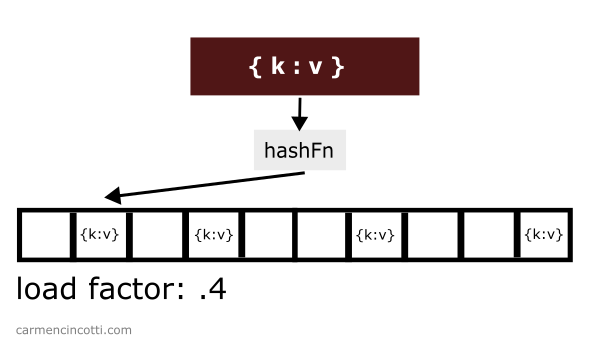
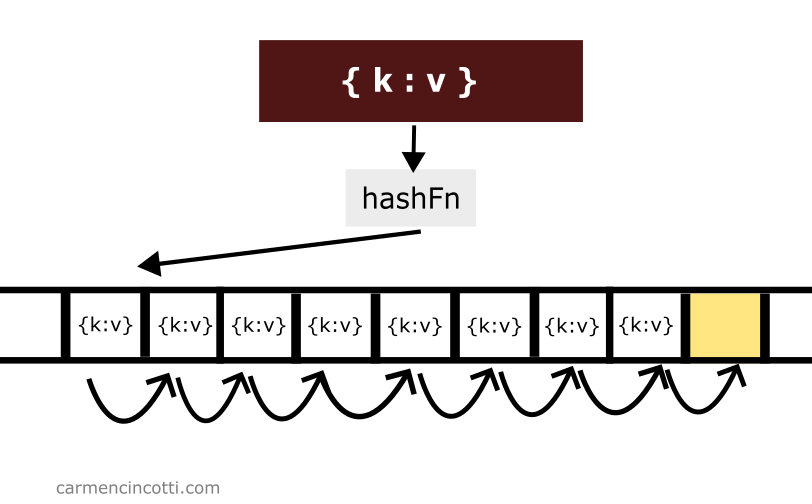
Chaque élément est placé dans la table de hachage en recherchant (ou en sondant comme nous l’appellerons) un seau ouvert pour le placer. Voici un exemple :
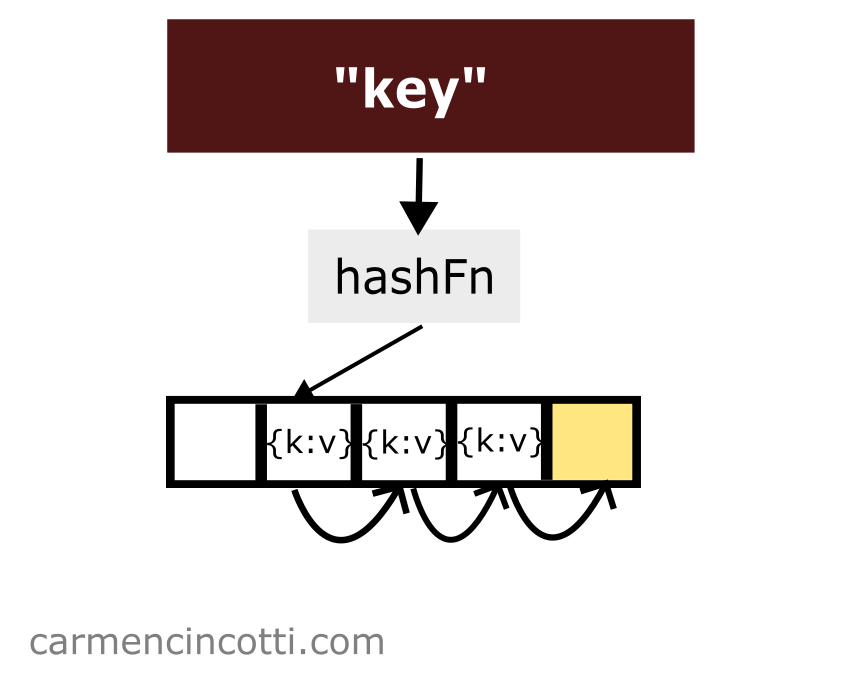
Comment est-ce possible ? Pour mieux comprendre, nous devons d’abord en savoir plus sur le sondage.
Qu’est-ce que le sondage ?
Le sondage est le moyen permettant de trouver un seau ouvert, ou un élément déjà stocké, dans le tableau sous-jacent d’une table de hachage.
Il existe quelques méthodes populaires pour ce faire. Chaque méthode a des avantages et des inconvénients, comme nous le verrons.
- Le sondage linéaire : On recherche un seau ouvert ou occupé séquentiellement dans la table de hachage.
- Le sondage quadratique : On recherche un seau ouvert ou occupé de manière quadratique dans la table de hachage.
- Le double hachage : On recherche un seau ouvert ou occupé dans la table de hachage tout en hachant deux fois une clé.
Comment grandir une table de hachage au fil du temps ?
Pour augmenter la taille d’une table de hachage, nous profitons de deux astuces pour nous aider - le facteur de charge et un processus connu sous le nom de rehachage (rehashing).
Le facteur de charge
Le facteur de charge mesure le degré de remplissage d’une table de hachage.
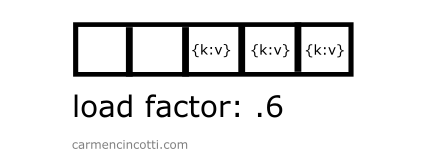
Il est défini comme où est le nombre d’éléments dans la table et est la taille de la table de hachage.
Par conséquent, à mesure que nous augmentons la quantité d’éléments dans la table de hachage, le facteur de charge augmentera …
Cela entraînera sans aucun doute une augmentation des temps d’accès à la table de hachage avec le temps en raison de la résolution des collisions de hachage.
Mais tout n’est pas perdu. Pour nous aider à maintenir des vitesses d’accès fulgurantes, il faut définir un seuil de facteur de charge… qui, une fois dépassé, déclenchera un processus dans la table de hachage appelé le rehachage (rehashing), que nous verrons maintenant.
Le rehachage
Quand le seuil du facteur de charge est franchi, on doit augmenter la taille du tableau sous-jacent… généralement, on double la taille lors de ce processus. Prenons cet exemple où j’ai une table de hachage avec un seuil de facteur de charge défini sur .
Il y a déjà trois éléments stockés dans la table tandis que la taille de la table elle-même est . Le facteur de charge est donc .
Si j’ajoute un élément de plus à cette table :
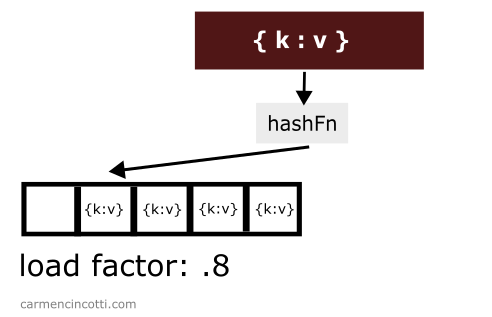
Le facteur de charge franchira le seuil ! Il faudra à cet instant doubler sa taille afin de réduire le facteur de charge :
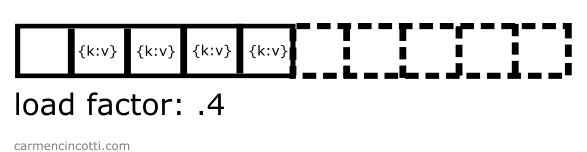
À ce stade, il faudra rehacher tous les éléments et les remettre dans la table.
Ce processus est cher. C’est pour cela que nous n’effectuons ce processus qu’au franchissement du seuil de facteur de charge.
La complexité temporelle
La complexité temporelle d’un tel processus est . Cependant, ce processus ne se produit qu’une fois de temps en temps.
C’est pourquoi qu’on dirait que nous bénéficions pour la plupart du temps d’une complexité temporelle de que la table de hachage fournit. Dans ce cas, on dit que la complexité temporelle est amortie à .
Sondage linéaire
Le sondage linéaire est un moyen de résoudre les collisions de hachage en recherchant séquentiellement un emplacement ouvert jusqu’à ce qu’on en trouve un.
La formule
La formule est la suivante :
où est l’indice du tableau sous-jacent, est la fonction de hachage, est la clé et est l’itération de la sonde. est la taille de la table.
Opérations courantes
Les opérations courantes d’une table de hachage qui implémente le sondage linéaire sont similaires à celles d’une table de hachage qui implémente un chaînage séparé.
Nous verrons ce que cela signifie dans les sections suivantes.
Insertion
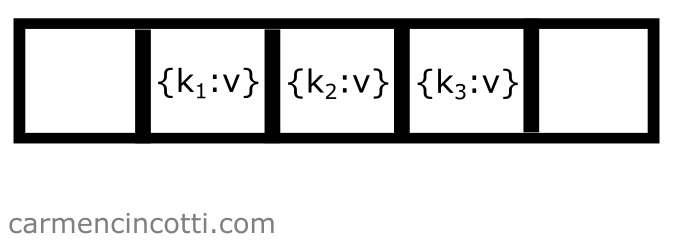
Prenons l’exemple suivant - nous avons un tableau sous-jacent déjà rempli avec quelques éléments :
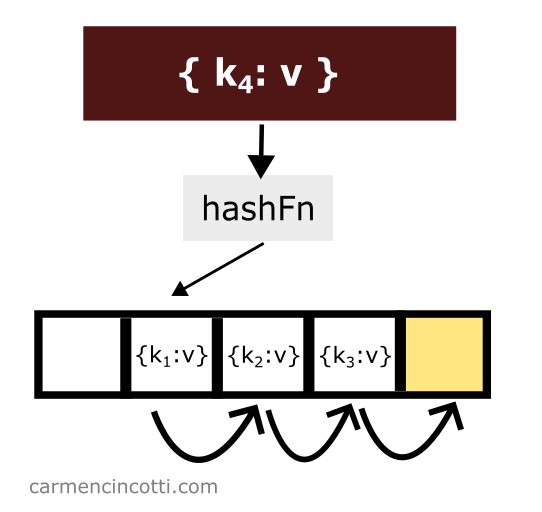
Si nous voudrions ajouter un autre élément à la table avec la clé qui est hachée au même emplacement qu’un autre élément, nous ne devons que parcourir le tableau sous-jacent jusqu’à ce que nous trouvions un seau ouvert afin de placer l’élément dans la table :
Recherche
Le sondage linéaire fonctionne comme son nom l’indique. Il y a une sonde qui parcourt linéairement le tableau sous-jacent. S’il trouve un élément d’intérêt dans son chemin en parcourant le tableau - il le renverra à l’utilisateur.
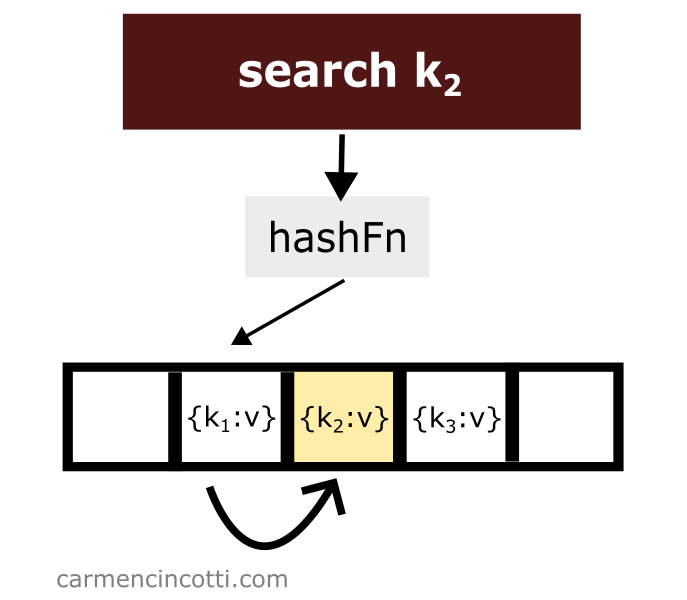
Cependant, s’il trouve un seau vide lors de sa recherche, il s’arrêtera à ce moment et signalera à l’utilisateur qu’il n’a rien trouvé.
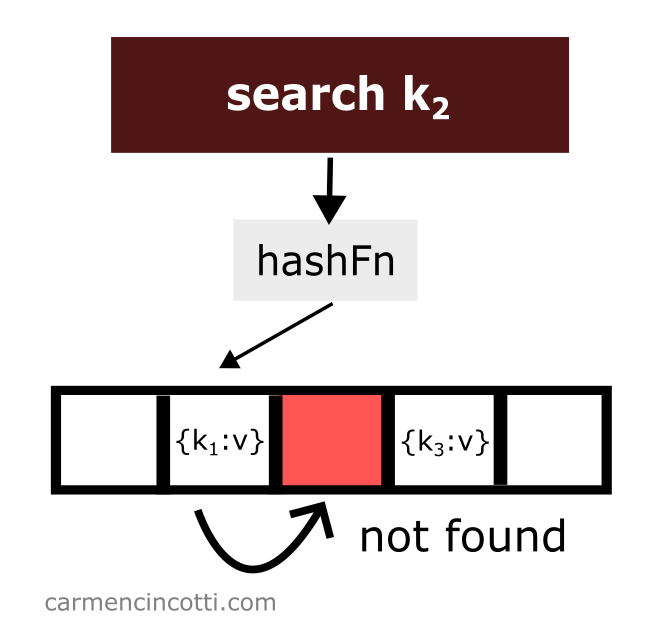
Ce qui soulève la question : que se passera-t-il si nous supprimons un élément ? 🤔
Suppression
La suppression d’un élément tout en utilisant le sondage linéaire est un peu délicate. Considérons cet exemple où je supprime naïvement un élément d’une table de hachage :
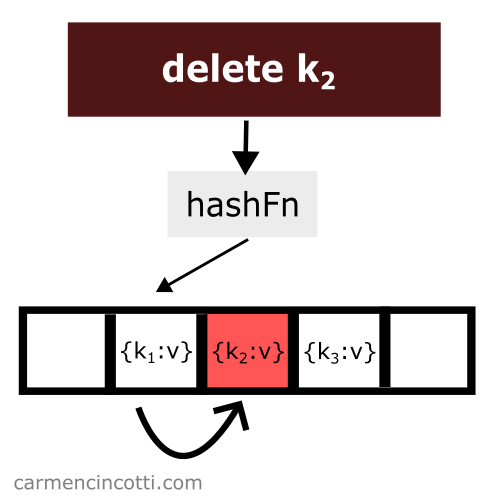
Nous venons de supprimer un élément de la table de hachage. Ensuite, on recherche l’élément qui est haché par la fonction de hachage au même emplacement que l’élément qui vient d’être supprimé et qui a été placé plus tôt dans la table de hachage à droite par rapport à l’élément qui vient d’être supprimé :
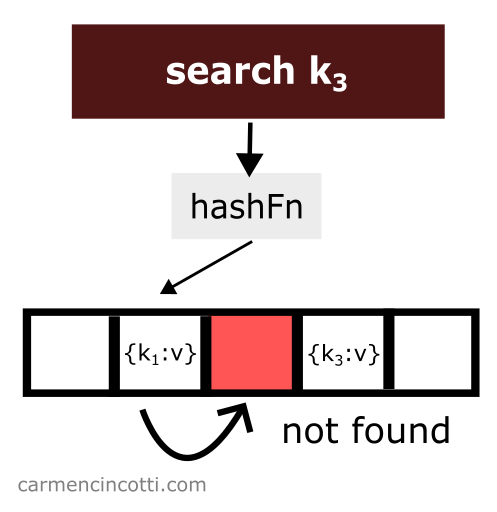
Nous ne le trouverons pas ! Pourquoi ? 🤔
Car la sonde linéaire s’arrête lorsqu’elle rencontre un seau vide.
Pour éviter un tel comportement imprévu - il faut placer à l’endroit de la suppression d’un élément ce qui est appelé une pierre tombale (ou tombstone en anglais) 🪦.
Si la sonde linéaire rencontre une pierre tombale lors de la recherche dans le tableau, elle l’ignorera et continuera sa recherche de l’élément que nous voulons.
Voyons un exemple avec cette idée en tête :
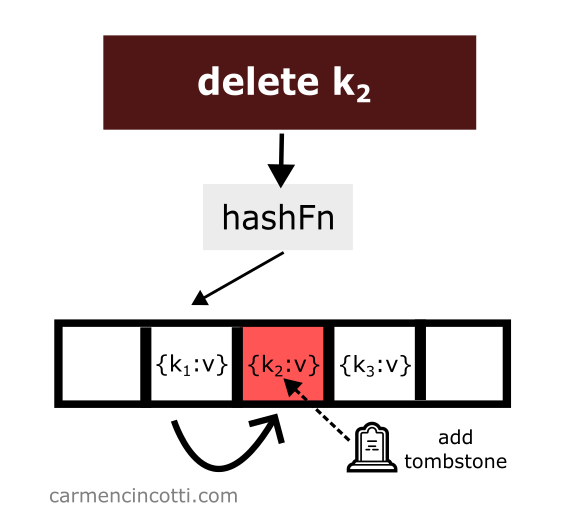
On vient de supprimer un élément tout en plaçant une pierre tombale à sa place.
Ensuite, on recherche un élément comme avant, mais cette fois on arrive à le retrouver grâce à la pierre tombale :

Les inconvénients
Il y a quelques inconvénients lorsqu’on utilise le sondage linéaire pour maintenir une table de hachage. Jetons un coup d’œil ensemble !
Clustering primaire
Le sondage linéaire est sensible à un phénomène qui s’appelle clustering primaire.
Le clustering primaire est un phénomène qui se produit lorsque des éléments sont ajoutés à une table de hachage. Les éléments peuvent avoir tendance à s’agglutiner, à former des clusters, ce qui, au fil du temps, aura un impact significatif sur les performances de recherche et d’ajout d’éléments, car nous approcherons le pire des cas complexité temporelle.
On dirait que le sondage linéaire est un moyen efficace de remplir une table de hachage si la table n’est pas trop remplie !
Maintenance
Lors de la durée de vie d’une table de hachage, il faut maintenir le tableau sous-jacent afin d’éviter des problèmes de surstockage.
Comme nous l’avons déjà vu, si le tableau est trop plein, on risque de dégrader la complexité temporelle de à .
Pour éviter ce problème, nous devrions suivre le facteur de charge.
Les avantages
Il y a également quelques avantages à utiliser une telle structure.
Les performances de cache
Grâce au fait que le sondage linéaire parcourt le tableau sous-jacent de manière linéaire, il profite de performances de cache plus élevées par rapport à d’autres formes d’implémentations de table de hachage.
Simplicité
Il faut dire que la complexité de trouver un espace ouvert est facile parce que la sonde parcourt le tableau sous-jacent de manière linéaire.
Les autres méthodes, comme nous le verrons, sont sensibles aux cycles. Ce phénomène se produit lorsque la sonde répète son chemin en essayant de trouver un espace libre … et ce cycle ne se termine jamais !
