Cette semaine, j’aimerais poursuivre notre conversation sur l’adressage ouvert et des tables de hachage.
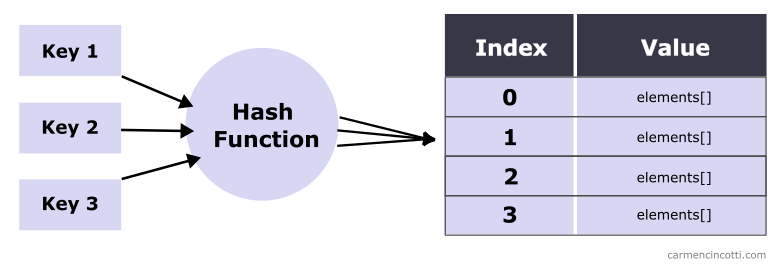
Plus précisément, on verra de plus près le sondage quadratique et son fonctionnement.
Rappelons-nous que la semaine dernière, nous avons parlé du sondage linéaire qui est un bon moyen de résoudre des collisions de hachage afin de rechercher et de placer des éléments dans une table de hachage.
Cela dit, plongeons-y en apprenant plus sur le sondage quadratique.
Salut ! Avant de continuer, je vous suggère que si vous n’avez pas déjà lu les articles précédents sur l’adressage ouvert et les tables de hachage, je vous recommande vraiment d’y jeter un coup d’œil afin de pouvoir suivre plus facilement :
Quelle est la différence entre le sondage linéaire et le sondage quadratique ?
Le sondage quadratique n’est pas une technique où la sonde parcourt le tableau de stockage sous-jacent de manière linéaire. Au contraire, il parcourt le tableau de stockage sous-jacent d’une manière quadratique.
Par exemple - voici comment la sonde linéaire parcourt le tableau de stockage sous-jacent de manière linéaire en plaçant un élément :
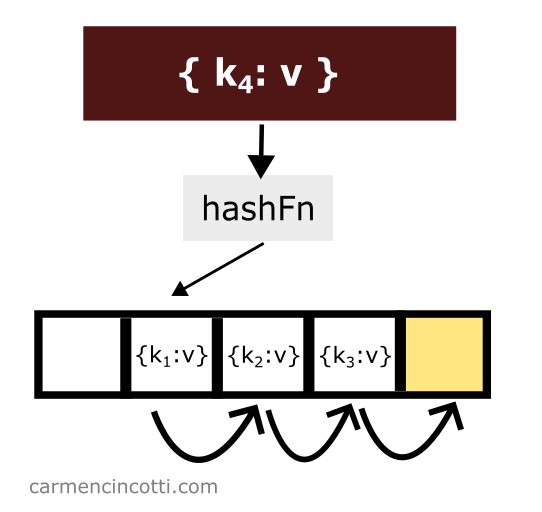
Ce concept de « parcourir du tableau de stockage sous-jacent de manière linéaire » est unique au sondage linéaire…
On verra mieux comment fonctionne le sondage quadratique au cours de cet article !
Qu’est-ce que le sondage quadratique ?
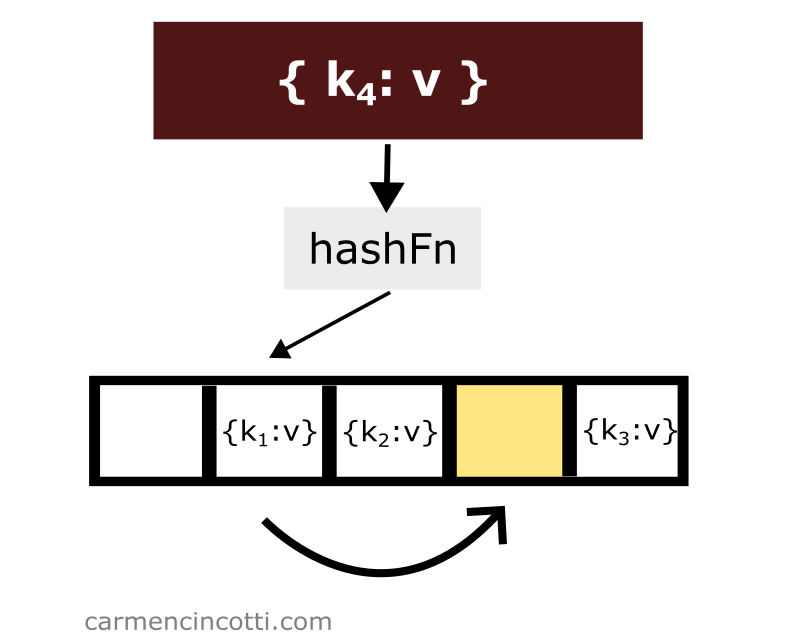
Le sondage quadratique est un moyen de résoudre les collisions de hachage en recherchant de manière quadratique un seau ouvert ou un élément spécifique jusqu’à ce qu’on en trouve un.
La formule
La formule du sondage quadratique pour trouver un seau ouvert ou un élément particulier déjà placé dans la table de hachage est la suivante :
où est l’indice du tableau sous-jacent, est la fonction de hachage, est la clé de l’élément à hacher. est la taille de la table… et de ?
La nouvelle variable avec laquelle nous devons nous familiariser est . est la fonction quadratique que nous devons définir et est x-ième itération du sondage. Rappelons qu’une fonction quadratique prend la forme : .
Voyons ce que cela signifie avec un exemple.
Un exemple
Prenons un exemple utilisant la fonction quadratique , et une taille de table .
J’ai aussi une table de hachage plutôt remplie, où les indices et dans le tableau de stockage sous-jacent sont déjà remplis :

J’aimerais insérer un élément qui est haché à l’indice - donc .
Pendant notre première itération de sonde - on verra une formule remplie avec les valeurs suivantes : , , :
Notre formule nous renvoie l’indice — mais on a déjà vu que cet emplacement dans la table de hachage est déjà occupé !

Il faut réessayer pour trouver un seau ouvert. Avant de continuer, nous devons d’abord itérer par . En faisant ceci, on calcule comme ceci : . La sonde est prête à réessayer :
Ça y est ! La sonde a trouvé un seau ouvert qui se trouve à l’indice :

On s’y achève !
Cycles
Le mot cycle est défini par Larousse comme suit :
Cycle : Suite de phénomènes se renouvelant dans un ordre immuable.
Comme le suggère cette définition, un cycle ne se termine jamais ! Ce phénomène se produit quand un chemin particulier est emprunté encore et encore sans fin lors de la recherche d’un seau ouvert ou d’un élément déjà placé dans la table de hachage.
Prenons un exemple pour bien comprendre ce que ceci signifie !
Un exemple
Reprenons la formule du sondage quadratique :
Lors de cet exemple, je vais définir la fonction quadratique, , comme , et la taille de la table, , comme .
J’ai aussi une table de hachage plutôt remplie, où les indices et sont déjà remplis :

J’aimerais insérer un élément qui est haché à l’indice - donc .
Pour notre première itération de sonde - on verra une formule remplie avec les valeurs suivantes : , , :
Cependant, l’indice n’est pas disponible, car un élément s’y trouve déjà !

Cela dit, on continue en augmentant la valeur afin de trouver un seau libre.
| x | H(k) | J(x) | i |
|---|---|---|---|
| 0 | 0 | 4 | 0 |
| 1 | 0 | 6 | 2 |
| 2 | 0 | 12 | 0 |
| 3 | 0 | 22 | 2 |
| 4 | 0 | 36 | 0 |
| 5 | 0 | 54 | 2 |
L’élément n’est jamais placé à cause d’un cycle !
Il faut donc faire attention afin d’éviter un tel phénomène lors du choix d’une fonction quadratique.
Comment éviter un cycle
Il y a de nombreuses méthodes et études pour trouver la meilleure fonction quadratique. Mes recherches ont conclu qu’il existe des règles simples que l’on peut suivre au début :
- , et gardez la taille de la table, , un nombre premier et aussi (le facteur de charge maximum) <= .
- , et gardez la taille de la table une puissance de deux : .
- , et garder la taille de la table, , un nombre premier N où N ≡ 3 mod 4.
Opérations courantes
Les opérations courantes d’une table de hachage qui implémente le sondage quadratique sont similaires à celles d’une table de hachage qui implémente le sondage linéaire.
Nous verrons ce que cela signifie dans les sections suivantes.
Insertion
Prenons l’exemple suivant - nous avons un tableau sous-jacent déjà rempli avec quelques éléments :
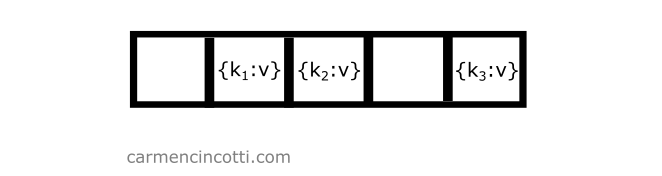
Si nous voudrions ajouter un autre élément à la table avec la clé qui est haché au même emplacement qu’un autre élément, nous ne devons que parcourir le tableau sous-jacent jusqu’à ce que nous trouvions un seau ouvert afin de placer l’élément dans la table :

Recherche
Le sondage quadratique fonctionne comme son nom l’indique. Il y a une sonde qui parcourt d’une manière quadratique le tableau sous-jacent. S’il trouve un élément d’intérêt dans son chemin en parcourant le tableau - il le renverra à l’utilisateur.
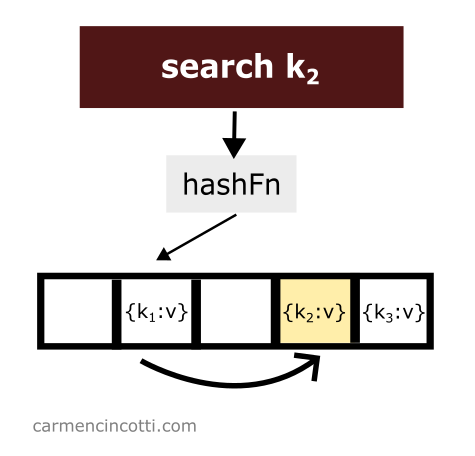
Cependant, s’il trouve un seau vide lors de sa recherche, il s’arrêtera à ce moment et signalera à l’utilisateur qu’il n’a rien trouvé.
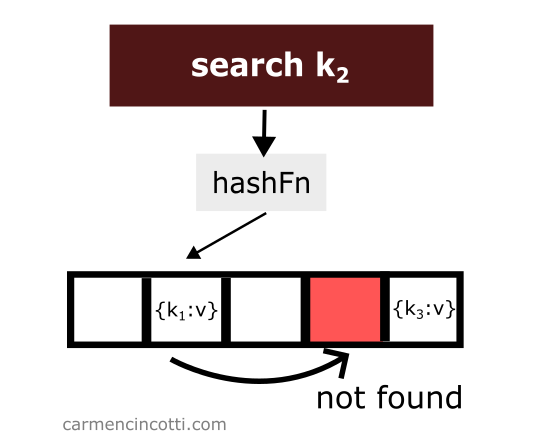
Ce qui soulève la question : que se passera-t-il si nous supprimons un élément ? 🤔
Suppression
La suppression d’un élément tout en utilisant le sondage quadratique est un peu délicate. Considérons cet exemple où je supprime naïvement un élément d’une table de hachage :
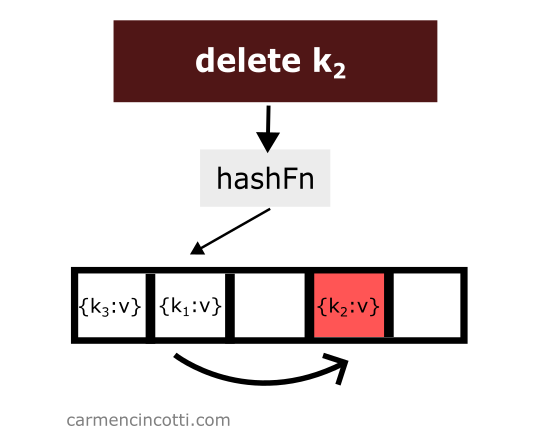
Nous venons de supprimer un élément de la table de hachage. Ensuite, on recherche l’élément qui est haché par la fonction de hachage au même emplacement que l’élément qui vient d’être supprimé et qui a été placé plus tôt dans la table de hachage à droite par rapport à l’élément qui vient d’être supprimé :
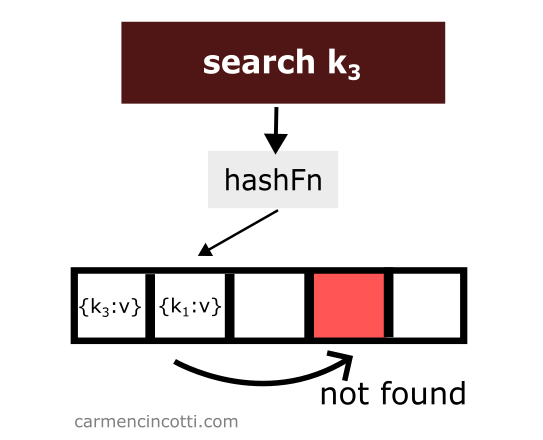
Nous ne le trouverons pas ! Pourquoi ? 🤔
Car la sonde quadratique s’arrête lorsqu’elle rencontre un seau vide.
Pour éviter un tel comportement imprévu - il faut placer à l’endroit de la suppression d’un élément ce qui est appelé une pierre tombale (ou tombstone en anglais) 🪦.
Si la sonde quadratique rencontre une pierre tombale lors de la recherche dans le tableau, elle l’ignorera et continuera sa recherche de l’élément que nous voulons.
Voyons un exemple avec cette idée en tête :
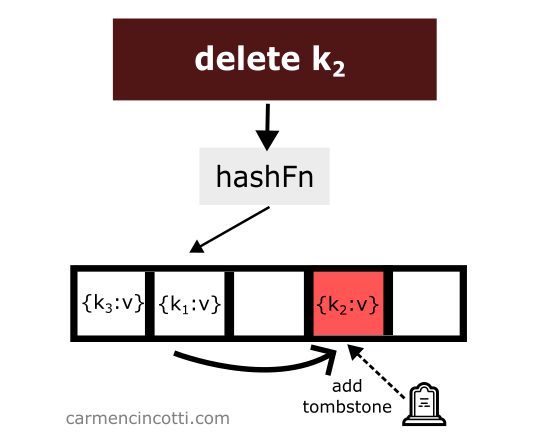
On vient de supprimer un élément tout en plaçant une pierre tombale à sa place.
Ensuite, on recherche un élément comme avant, mais cette fois on arrive à le retrouver grâce à la pierre tombale :
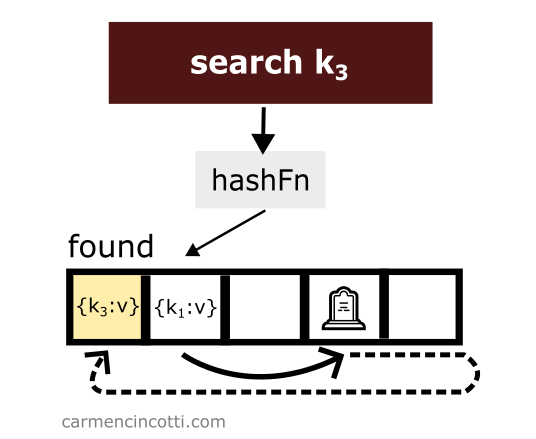
Inconvénients
Alors que le sondage quadratique évite les problèmes de clustering primaire, il y a un autre problème de clustering moins sévère - le clustering secondaire.
Le clustering secondaire
Le clustering secondaire est observé lors du remplissage d’une table de hachage avec de nombreux éléments qui se hachent vers le même seau ouvert.
Pour chaque élément qui se hache initialement vers le même seau, la sonde quadratique visitera de manière déterministe les mêmes seaux afin d’en trouver un qui est ouvert.
Pour chaque nouvel élément qui hache vers le même seau dans la table, il faudra suivre ce chemin à chaque fois, et ajouter le nouvel élément à ce chemin… ce qui fera grossir ce chemin avec le temps et donc aggraver le problème.
Performances de la cache
D’ailleurs, on perd un peu de l’efficience de cache dû au fait que pour trouver un espace libre nous devons parcourir le tableau de manière non linéaire.
Avantages
Évitement du clustering primaire
Heureusement, le sondage quadratique est moins sensible au clustering primaire que nous avons déjà vu lors de notre discussion sur le sondage linéaire.
Pour résumer, le clustering primaire est un phénomène qui se produit lorsque des éléments sont ajoutés à une table de hachage. Les éléments peuvent avoir tendance à s’agglutiner, à former des clusters, ce qui, au fil du temps, aura un impact significatif sur les performances de recherche et d’ajout d’éléments, car nous approcherons le pire des cas complexité temporelle.
Complexité temporelle
Pour résumer, une table de hachage nous donne une complexité temporelle plus efficiente par rapport à un tableau ou à une liste chaînée quand nous voudrions rechercher, insérer ou supprimer un élément (en moyenne).
| Structure | Access | Search | Insertion | Deletion |
|---|---|---|---|---|
| Array | ||||
| Linked List | ||||
| Hash Table |
Et dans le scénario du pire des cas, nous verrions ces complexités temporelles :
| Structure | Access | Search | Insertion | Deletion |
|---|---|---|---|---|
| Array | ||||
| Linked List | ||||
| Hash Table |
Pourquoi y a-t-il un cas pire ? C’est dû à des collisions de hachage. Il faut choisir un tableau sous-jacent suffisamment grand ainsi qu’un facteur de charge plutôt modéré.
