Double hachage | Adressage ouvert | Tables de hachage

Pour construire notre propre table de hachage spatiale, nous devrons comprendre comment résoudre les collisions de hachage que nous rencontrons lors de l'ajout d'éléments avec le double hachage.

Keywords: javascript, tutoriel, table de hachage spatiale, carte de hachage, structures de données, leetcode

By Carmen Cincotti

October 24, 2022

Qu’est-ce que le double hachage ?
Des ressources (en français et anglais)

Le double hachage utilise l’idée d’appliquer une deuxième fonction de hachage à la clé lorsqu’une collision se produit dans une table de hachage.

Une table de hachage

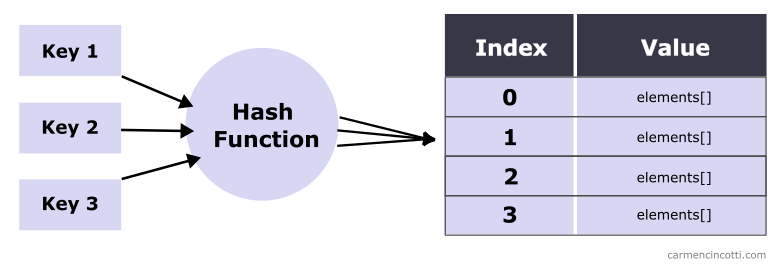
Nous examinerons de plus près le double hachage ainsi que la manière dont nous pouvons l’utiliser pour résoudre les collisions lors du remplissage d’une table de hachage. Nous verrons également que le double hachage évite les problèmes rencontrés par d’autres techniques de collision, comme le clustering.

Rappelons-nous que la semaine dernière, nous avons parlé du sondage quadratique, et avant cela du sondage linéaire. Ces méthodes de sondage sont de bons moyens de résoudre des collisions de hachage afin de rechercher des éléments et de les placer dans une table de hachage.

Cela dit, plongeons-y en apprenant plus sur le double hachage.

Salut ! Avant de continuer, je vous suggère que si vous n’avez pas déjà lu les articles précédents sur l’adressage ouvert et les tables de hachage, je vous recommande vraiment d’y jeter un coup d’œil afin de pouvoir suivre plus facilement :

Qu’est-ce que le double hachage ?

Le double hachage est un moyen de résoudre les collisions de hachage en utilisant une deuxième fonction de hachage à la clé.

Inserting a new key into the hash table

La formule

La formule de double hachage pour trouver un seau ouvert ou un élément particulier déjà placé dans la table de hachage est la suivante :

i = ( H(k) + x * J(k) ) \mod S

où $i$ est l’indice du tableau sous-jacent, $H$ est la fonction de hachage, $k$ est la clé de l’élément à hacher. $S$ est la taille de la table… et de $J$ ?

$J$ est une deuxième fonction de hachage (le double hachage hein ?). On lui fournit la clé de l’élément à hacher. On multiplie ce nombre par $x$ . $x$ correspond à la x-ième itération de la séquence.

Voyons ce que cela signifie avec un exemple.

Un exemple

Prenons un exemple utilisant la fonction de hachage $J(k) = 3 - (k \mod 3)$ , et une taille de table $S = 4$ . Supposons que $k$ est un entier.

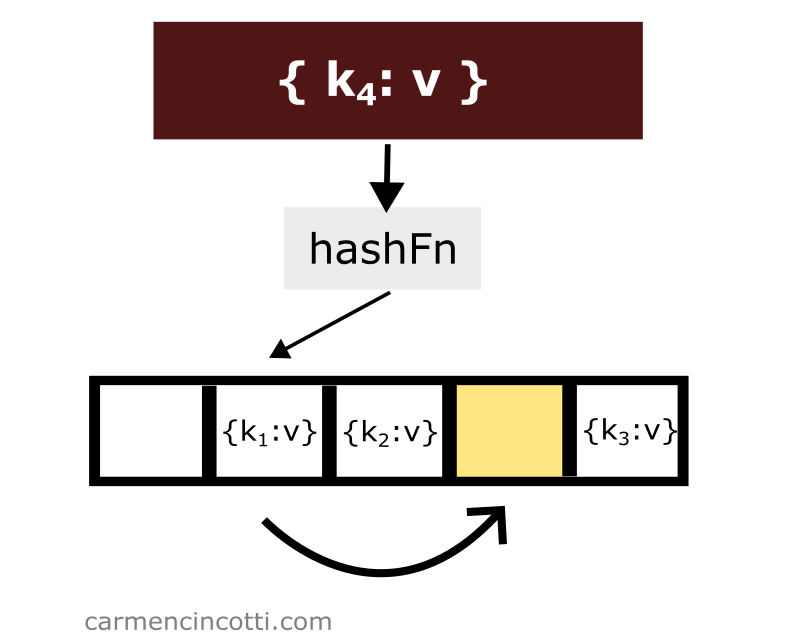
J’ai également une table de hachage plutôt complète : les indices $0$ et $3$ dans le tableau de stockage sous-jacent sont déjà occupés :

A hash table with some elements

J’aimerais insérer un élément avec une clé, $k = 10$ , qui est hachée à l’indice $0$ - donc $H(10) = 0$ .

Lors de notre première itération de la séquence de double hachage - on verra une formule remplie avec les valeurs suivantes : $H(10) = 0$ , $J(10) = 3 - 10 \mod 3 = 2$ , $S = 4$ , $x = 0$ :

i = 0 + 0 * 2 \mod 4 = 0

Notre formule nous renvoie l’indice $0$ — mais on a déjà vu que cet emplacement dans la table de hachage est déjà occupé !

Inserting a new key into the hash table - occupied bucket found

Il faut réessayer pour trouver un seau ouvert. Avant de continuer, nous devons d’abord itérer $x$ par $1$ . En faisant ceci, on calcule $x * J(k)$ comme ceci : $1 * J(10) = 1 * 2 = 2$ . Notre prochain calcul de $i$ est le suivant :

i = 0 + 1 * 2 \mod 4 = 2

Ça y est ! La sonde a trouvé un seau ouvert qui se trouve à l’indice $2$ :

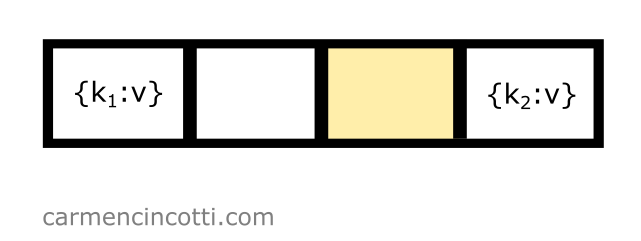
Inserting a new key into the hash table - open bucket found

On s’y achève !

Cycles

Rappelons qu’un cycle est une série qui ne se termine jamais. Ce phénomène se produit lorsqu’un chemin particulier est emprunté indéfiniment lors de la recherche d’un seau ouvert ou d’un élément déjà placé dans la table de hachage.

Pour voir comment un cycle se produit, je vous recommande de regarder cet exemple de l’article sur le sondage quadratique.

Le double hachage est-il sensible aux cycles ?

*Oui, le double hachage est sensible aux cycles.

Comment les éviter ?

Un bon moyen d’éviter les cycles est de choisir avec soin la deuxième fonction de hachage, $J(k)$ et la taille de la table $S$ . TopCoder nous recommande d’utiliser les conditions suivantes pour faire cela :

$S$ est un nombre premier
$J(k) = H_2(k) \mod S$
$J \geq 1$ et $J < S$

où $H_2(k)$ est une deuxième fonction de hachage.

L’astuce est que si ces conditions sont satisfaites, nous pouvons nous assurer que la séquence de sondage va être de l’ordre N, ce qui nous fait atteindre chaque emplacement de notre table de hachage.

Opérations courantes

Les opérations courantes d’une table de hachage qui implémente le double hachage sont similaires à celles d’une table de hachage qui implémente d’autres techniques d’adresse ouverte telles que le sondage linéaire ou quadratique.

Nous verrons ce que cela signifie dans les sections suivantes.

Insertion

Insérer un élément dans une table de hachage en utilisant le double hachage pour résoudre les collisions de hachage est une tâche facile !

Considérons l’exemple suivant où nous avons un tableau sous-jacent déjà rempli avec quelques éléments :

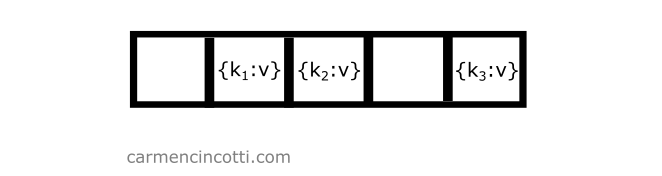
Hash table with elements at certain positions

Si nous souhaitons ajouter un autre élément à la table avec la clé $k_4$ qui est hachée au même emplacement qu’un autre élément, nous ne devons que parcourir le tableau sous-jacent jusqu’à ce que nous trouvions un seau ouvert afin de placer l’élément dans la table :

Inserting a new key into the hash table

Pour faire cela, rappelons de la formule $i = ( H(k) + x * J(k) ) \mod S$ . On itère $x$ afin de parcourir le tableau.

Recherche

La séquence à suivre qui est définie par la formule de double hachage fonctionne comme les sondes dont nous avons déjà parlé. On parcourt le tableau sous-jacent en recherchant l’élément d’intérêt :

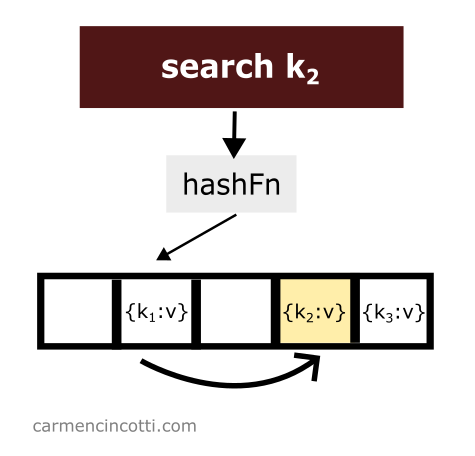
Searching for an element

Tout va bien si l’élément d’intérêt est trouvé par la sonde !

Cependant, si un seau vide est trouvé lors de la recherche, la recherche s’arrêtera à ce moment. Rien n’a été trouvé :

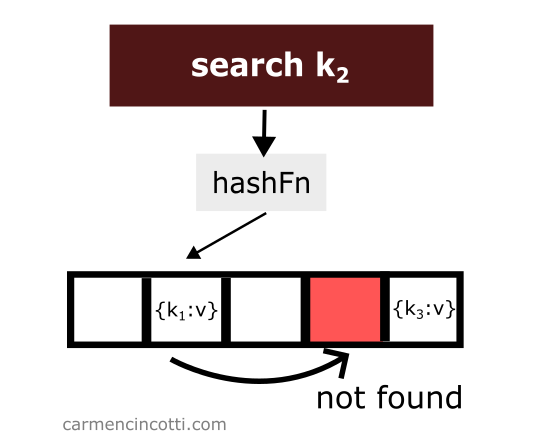
Searching for an element and hitting an empty location

Ce qui soulève la question : que se passera-t-il si nous supprimons un élément ? 🤔

Suppression

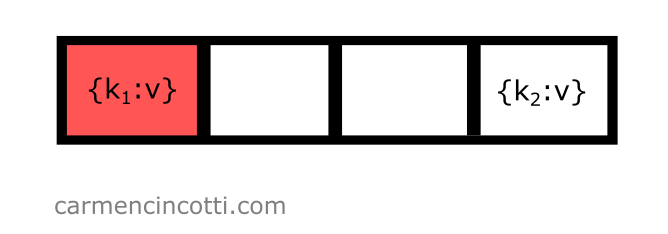
Supprimer un élément tout en utilisant le double hachage est un peu délicat. Considérons cet exemple où je supprime naïvement un élément d’une table de hachage :

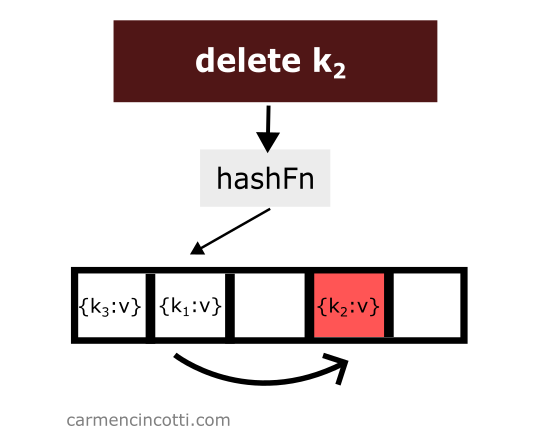
Delete an element from hash table

Nous venons de supprimer un élément de la table de hachage. Ensuite, on recherche l’élément qui est haché par la fonction de hachage au même emplacement que l’élément qui vient d’être supprimé et qui a été placé plus tôt dans la table de hachage à droite par rapport à l’élément qui vient d’être supprimé :

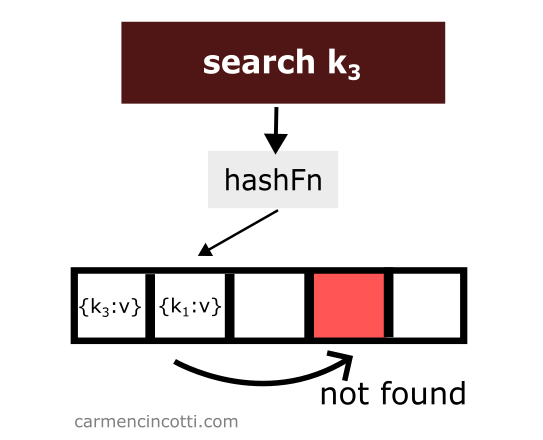
Search for an element from hash table that has been deleted incorrectly

Nous ne le trouverons pas ! Pourquoi ? 🤔

Parce que la séquence de double hachage s’arrête lorsqu’elle rencontre un seau vide.

Pour éviter un tel comportement imprévu - il faut placer à l’endroit de la suppression d’un élément ce qui est appelé une pierre tombale (ou tombstone en anglais) 🪦.

Si la séquence de double hachage rencontre une pierre tombale lors de la recherche dans le tableau, elle sera ignorée et la séquence se poursuivra.

Voyons un exemple avec cette idée en tête :

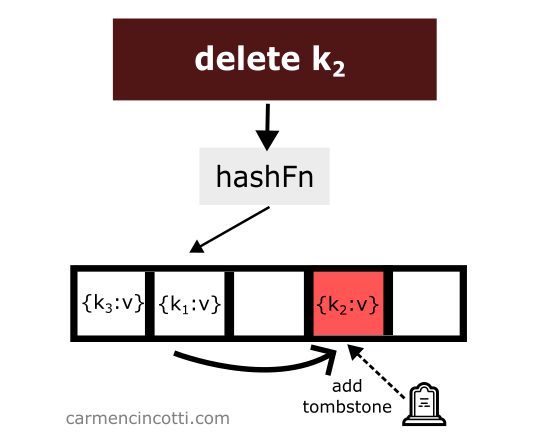
Delete an element from hash table and place a tombstone

On vient de supprimer un élément tout en plaçant une pierre tombale à sa place.

Ensuite, on recherche un élément comme avant, mais cette fois on arrive à le retrouver grâce à la pierre tombale :

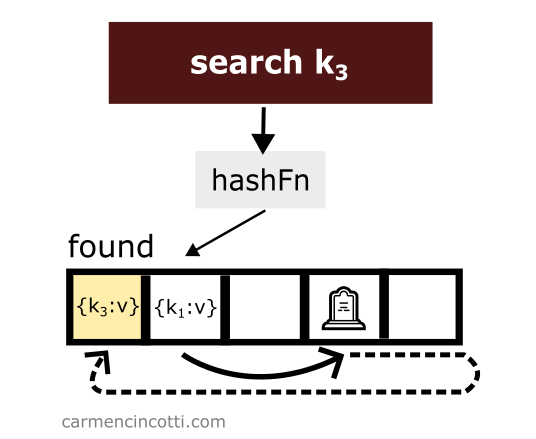
Search and find the element after deleting correctly with a tombstone

Inconvénients

Bien que le double hachage évite les problèmes de clustering, il paie pour ce luxe en souffrant de cache ratée.

Performances de la cache

Le double hachage agit comme une liste chaînée. C’est-à-dire du point de vue du CPU, la séquence est presque pseudoaléatoire. Cela rendrait la cache presque inutile…

Avant de continuer, il faut dire que la recherche suggère que le double hachage est toujours préférable au sondage linéaire et au sondage quadratique parce qu’il évite totalement le clustering, ce qui donne au double hachage un véritable gain de performances.

Avantages

Évitement du clustering

Le clustering primaire

Heureusement, le double hachage évite le clustering primaire que nous avons déjà vu lors de notre discussion sur le sondage linéaire.

Pour résumer, le clustering primaire est un phénomène qui se produit lorsque des éléments sont ajoutés à une table de hachage. Les éléments peuvent avoir tendance à s’agglutiner, à former des clusters, ce qui, au fil du temps, aura un impact significatif sur les performances de recherche et d’ajout d’éléments, car nous approcherons le pire des cas $O(n)$ complexité temporelle.

Le cluster secondaire

Le double hachage évite également le clustering secondaire que nous avons déjà vu lors de notre discussion sur le sondage quadratique

Pour résumer, le clustering secondaire se produirait si chaque nouvel élément qui hache vers le même seau dans la table doit suivre le même chemin. Ce phénomène va donc amener les éléments à s’ajouter à ce chemin lorsqu’il trouve un espace vide… ce qui fera grossir ce chemin avec le temps et donc aggraver encore le problème.

Complexité temporelle

Pour résumer, une table de hachage nous donne une complexité temporelle plus efficiente par rapport à un tableau ou à une liste chaînée quand nous voudrions rechercher, insérer ou supprimer un élément (en moyenne).

Structure	Access	Search	Insertion	Deletion
Array	$O(1)$	$O(n)$	$O(n)$	$O(n)$
Linked List	$O(n)$	$O(n)$	$O(1)$	$O(1)$
Hash Table	$O(1)$	$O(1)$	$O(1)$	$O(1)$

Et dans le scénario du pire des cas, nous verrions ces complexités temporelles :

Structure	Access	Search	Insertion	Deletion
Array	$O(1)$	$O(n)$	$O(n)$	$O(n)$
Linked List	$O(n)$	$O(n)$	$O(1)$	$O(1)$
Hash Table	$O(n)$	$O(n)$	$O(n)$	$O(n)$

Pourquoi y a-t-il un cas pire ? C’est dû à des collisions de hachage. Il faut choisir un tableau sous-jacent suffisamment grand ainsi qu’un facteur de charge plutôt modéré.

Carmen's Graphics Blog