Cette semaine, j’ai continué à mieux connaître les éléments nécessaires pour créer une scène 3D avec WebGPU. Je suis arrivé au point où je voulais introduire la possibilité de bouger la caméra. En fait, lors de sa mise en place, je me suis vite rendu compte que la théorie d’une caméra 3D n’est pas anodine. La théorie est une passerelle vers les connaissances nécessaires pour comprendre comment créer et multiplier des matrices transformatrices pour mettre en scène nos objets 3D.

⚠️ Cet article est la suite de notre discussion de la semaine dernière. Je vous recommande de le relire pour mieux comprendre le contexte de contenu que l’on va voir !

La Caméra

La composition, la mise en scène et les mouvements de caméra sont les fondations d’une histoire.

La caméra est la porte d’entrée de notre scène 3D. Sans elle, nos scènes seraient ternes et plates sans la capacité de distinguer entre les éléments au premier plan et à l’arrière-plan, parmi une énorme liste d’autres choses.

Les caméras 3D ne sont pas réelles dans le sens où elles sont créées en appelant une fonction WebGPU. Pour les simuler, il faut les modéliser en utilisant soigneusement des matrices pour manipuler nos sommets 3D. Après avoir appliqué une série de matrices transformatrices aux sommets, nous pouvons voir notre monde à travers l’objectif de la caméra.

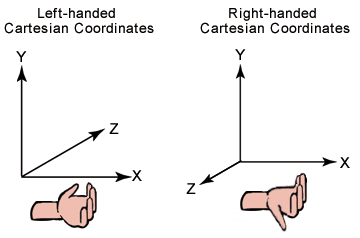
Un petit mot sur quelques suppositions concernant notre système de coordonnées… c’est un système de coordonnées droitier qui s’illustre sur l’image ci-dessous :

Ceci dit donc, on suppose que dans l’espace monde :

• l’axe X pointe vers la droite.
• l’axe Y pointe vers le haut.
• l’axe Z pointe vers l’écran (nous).

Mais, note bien la différence de la supposition dans l’espace de la caméra :

• l’axe X pointe vers la droite.
• l’axe Y pointe vers le haut.
• l’axe Z pointe vers la scène (pas vers nous) qui est au contraire de l’espace monde ! Il est donc négatif par rapport au système de coordonnées de monde. On voit vers l’axe négatif.

Alors, pour commencer, je propose d’étudier d’abord l’œil d’une caméra. De plus, nous devons également apprendre à créer la matrice nécessaire pour transformer la position de nos sommets d’espace monde en espace de la caméra.

L’œil et la matrice de vue

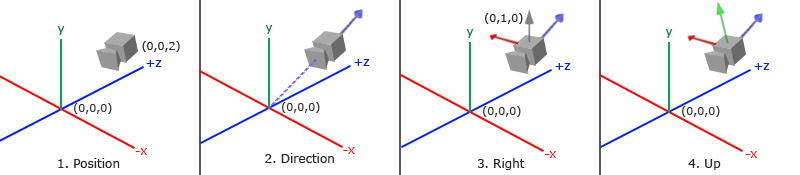
L’œil (eye) est à l’origine de notre caméra. On voit la scène à partir de ce point dans l’espace 3D. Notre but est de transformer notre scène de l’espace monde a l’espace de la caméra (espace de vue) ce qui signifie qu’on doit transformer notre système de coordonnées pour qu’il soit relatif à l’objectif de la caméra avec une matrice de transformation qui est connue sous le nom de matrice de vue. Une méthode pour construire la matrice de vue consistera à construire une matrice lookAt, qui encode la position et la cible de la caméra à travers des matrices de translation et de rotation.

La matrice lookAt

Nous pouvons calculer la direction et la rotation de notre caméra et construire une matrice afin de transformer notre système de coordonnées d’espace monde en espace de la caméra. Il faut trouver nos vecteurs de la caméra pour construire notre matrice de rotation.

Vecteur avant (l’axe z)

Pour calculer le forwardVector dans lequel notre axe avant de notre caméra pointe vers, il faut juste soustraire le vecteur positionnel de l’œil de la caméra du vecteur de position de notre cible. Supposons que la caméra pointe vers l’origine (0, 0, 0).

⚠️ NB. N’oubliez pas de normaliser ce vecteur résultant, car un vecteur directionnel est un vecteur unitaire.

⚠️ NB2. La direction qu’on vient de calculer est l’inverse de la ‘vraie’ direction, car l’axe z de notre caméra est à l’opposé du monde !

Vecteur droit (l’axe x)

En utilisant une petite astuce, nous pouvons trouver le vecteur directionnel rightVector en calculant le produit croisé entre le forwardVector et un vecteur arbitraire dirigé vers le haut. Un choix facile, c’est le vecteur directionnel (0, 1, 0). Le résultat sera un vecteur perpendiculaire pointant vers la droite, qui sera nôtre rightVector.

Rappelez-vous que le produit croisé peut être utilisé pour trouver un vecteur perpendiculaire à deux vecteurs dans l’espace 3D :

Nous pouvons tirer parti de ce fait pour choisir un tempUpVector, car il devrait théoriquement être dans le plan formé par le vrai upVector et le forwardVector :

Par conséquent, notre calcul devient :

Vecteur vers le haut (l’axe y)

Enfin, on utilisera l’astuce qu’on vient d’utiliser pour calculer le upVector de notre caméra. Cette fois, on croise notre rightVector et notre forwardVector.

Le vecteur de translation

Le calcul du vecteur translation de la caméra n’est pas suffisamment documenté dans les ressources que j’ai lues. Il faut utiliser le produit scalaire (dot) entre les vecteurs calculés et la position de l’œil. Fais attention parce que les ressources sont nombreuses, mais pas correctes !

Il est calculé de cette façon en raison de l’ordre des opérations matricielles. On fait d’abord la rotation, puis la translation. Il est donc nécessaire de calculer la translation de la caméra par rapport à sa nouvelle orientation.

Par exemple, supposons que notre caméra est placée à (0, 4, 4) dans l’espace monde. Il ne suffit pas de mettre le vecteur de translation à (0, 4, 4) comme ceci :

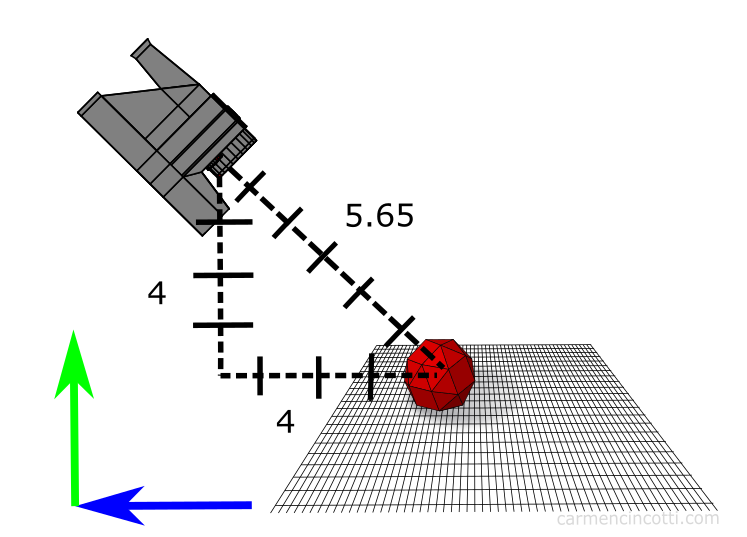
Au lieu de cela, nous devons d’abord appliquer la rotation, puis trouver le vecteur de translation, qui après avoir utilisé nos calculs de produit scalaire ci-dessus, nous constatons que cela correspond à un vecteur (0, 0, 5,65) :

La matrice lookAt finale

Enfin, la matrice finale :

Notre matrice finale est la suivante :

où R = rightVector, U = upVector et F = forwardVector.

Cependant, dans le code, la rotation et la translation sont inversées puisque rappelons qu’un ViewMatrix déplace en fait le monde pour faire de la caméra l’origine… faites attention, car cela m’a vraiment foutu au boulot un jour… l’inverse de la matrice rotation est sa ‘transpose’, et enfin l’inverse d’une translation est juste elle-même, mais négatif (dans l’autre sens)… donc notre viewMatrix est juste l’inverse de la matrice lookAt :

Code d’implémentation

En utilisant la matrice LookAt comme matrice de vue, nous transformerons toutes les coordonnées de l’espace monde à l’espace de notre caméra, où la caméra regarde vers l’axe z négatif.

Après avoir calculé la matrice de vue, la prochaine matrice à calculer est la matrice de projection. Pour ce faire, nous devons d’abord examiner les deux types de caméras sur lesquelles je voudrais me concentrer, à savoir la caméra perspective et la caméra orthographique.

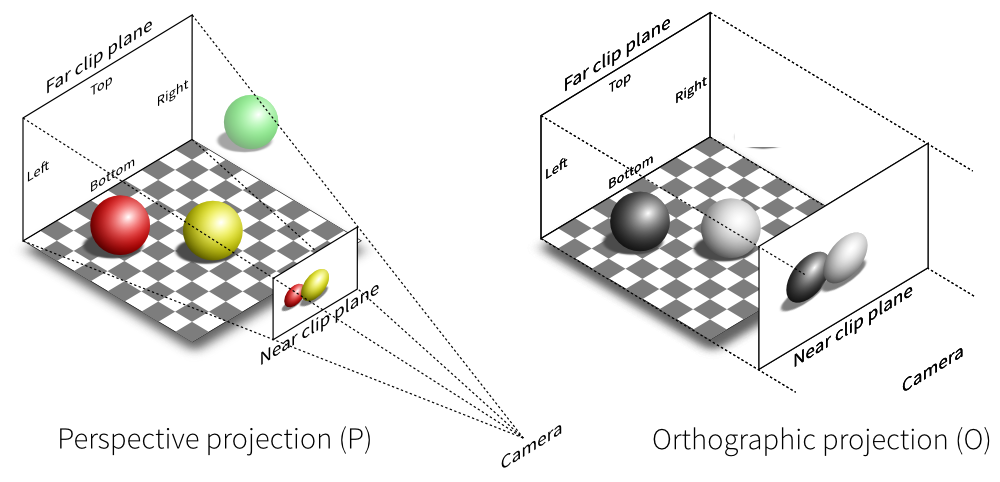
La caméra perspective

Une caméra perspective permet de distinguer la position des éléments en profondeur. Grâce à la projection, les objets éloignés sont plus petits que ceux qui sont proches. Nos yeux imitent cette vue. Imaginons que nous regardons une forêt, les arbres les plus proches nous paraissent plus gros que les arbres à quelques kilomètres.

By Wing-Chi Poon - self-made, at Gotier Trace Road, Bastrop State Park, Texas, USA. This area of Texas is known as the Lost Pines Forest., CC BY-SA 2.5, Link

Le modèle d’une caméra perspective

Ci-dessus est une illustration de la géométrie de la caméra qui s’appelle le frustum de vue. Les sommets à l’extérieur du frustum sont clippés (on y reviendra plus tard). La caméra perspective est composée de quelques parties qui doivent être définies afin de créer notre matrice de projection. Voici ces parties :

• Plan near (proche) - c’est la distance au near plan de clipping à travers l’axe z négatif (dans espace de la caméra)
• Plan far (lointain) - c’est la distance au far plan de clipping à travers l’axe z négatif (dans espace de la caméra)
• Champ de vision (fov_y) - c’est l’angle entre les côtés en haut et en bas du frustum.
• Le rapport d’aspect - c’est le rapport d’aspect de notre fenêtre.

Je te recommande de voir cette ressource pour jouer avec les paramètres différents afin de voir comment le frustum de vue marche.

💡 Les deux plans de clipping (near et far), sont-ils définis arbitrairement ?

La définition de ces deux plans est responsable de l’empêchement (ou de la cause) du z-fighting qui est dû à des problèmes de comparaison en virgule flottante.

Prenons un exemple artificiel afin de comprendre ce phénomène. Je place :

• Objet 1 dans l’espace caméra @ (0, 0, 50)
• Objet 2 @ (0, 0, 55)

…et je définis le plan proche (near) et le plan lointain (far) du frustum de vue comme étant 0,1 et 100.

À la base, une fois qu’on transforme nos coordonnées en NDC (on l’apprendra plus dans le prochain article), nos coordonnées dans le tampon Z sont placées entre 0 et 1 (l’axe Z dans NDC est défini comme ceci dans WebGPU - assurez-vous de vérifier ces valeurs si vous utilisez une API graphique différente).

Mes objets dans NDC sont donc définis comme:

• Objet 1 : (0, 0, 0,5)
• Objet 2 : (0, 0, 0,55)

Ces points devraient fonctionner sans problème et le z-fighting ne se produira pas, car la précision de ces valeurs n’est pas si précise que les problèmes de la comparaison entre virgule flottante se poseraient.

Ensuite, plaçons le plan proche (near) sur 1e-5 et le plan lointain (far) sur 1e6. Maintenant dans NDC, on commence à remarquer que la précision est plus importante :

• Objet 1 sera situé à (0, 0, 0,00004)
• Objet 2 sera situé à (0, 0, 0,000045)

Comme vous pouvez le voir, nous commençons maintenant à exiger beaucoup de la part de notre ordinateur mauvaise capacité à comparer la virgule flottante super précise (spoiler : ce n’est pas si génial) …

This will certainly cause problems, thus it is important to use reasonable values.

La caméra orthographique

Avec la caméra orthographique, tous les objets égaux apparaissent à la même échelle. Les lignes parallèles restent parallèles qui sont différentes de notre caméra perspective. Cela permet de juger plus facilement les tailles relatives et l’alignement des modèles.

Tout comme le modèle de la caméra perspective, on définit des paramètres afin de la configurer. Nous sommes responsables de définir le plan proche et le plan lointain, ainsi que les autres plans qui forment le cube de projection orthogonale.

Parce que je vais me concentrer davantage sur les caméras perspectives dans un futur proche, je ne vais pas trop m’attarder sur les caméras orthographiques pour l’instant…

La suite

Dans l’article suivant, nous verrons plus en détail les transformations de nos coordonnées.

Des ressources (en français et anglais)

• Carmen Cincotti - The Magic of the LookAt Matrix
• Carmen Cincotti - Lets Look At Magic LookAt Matrices
• Brown37 - Introduction to Cameras
• Pearson Education France - Filmer avec un reflex numérique
• Prusa3d - Caméra perspective / orthographique
• Wellesley - Viewports, Aspect Ratio, Depth, Unprojection
• Dustin P Fister - Working with a perspective camera in three.js
• w3 - WebGPU - Coordinate Systems
• Developpez - Apprendre OpenGL moderne
• Brown37 - Perspective Projections