Coordonnées homogènes, espace de découpage, et NDC | WebGPU

Nous plongeons dans l'espace de découpage et NDC, et examinons de plus près les mathématiques de projection impliquées pour y arriver. Nous en apprendrons également plus sur les coordonnées homogènes.

Keywords: WebGPU, algèbre linéaire, la projéction, les coordonnées homogènes, le pipeline de rendu, le rendu en temps réel, les transformations

By Carmen Cincotti

May 02, 2022Updated November 21, 2022

Une révision de la caméra perspective
- 💡 Comment calculer la matrice de projection d’une caméra perspective
Les coordonnées homogènes.
- Les applications
  - La transformation projection
    - 💡 Est-ce que w = 1 tout le temps ?
  - La translation des coordonnées 3D
L’espace de découpage
- Comment entrer l’espace de découpage
- 💡 Et le triangle qui a des sommets à l’intérieur et à l’extérieur du volume de découpage ?
NDC
La suite
Des ressources (en français et anglais)

Cette semaine, j’ai continué à étudier les transformations nécessaires pour amener un sommet positionné dans l’espace du modèle 3D, sur notre écran 2D.

Avec la connaissance de la transformation de projection dans notre poche, nous pouvons enfin parler de l’espace de découpage et du NDC (coordonnées normalisées). Pour comprendre ces sujets, nous aurons également besoin de voir des coordonnées homogènes.

Une révision de la caméra perspective

Field of view angle in view frustum

Rappelons que la caméra perspective est modélisée comme une pyramide tronquée qui s’appelle le frustum de vue.

Ce frustum se compose de quelques parties qui doivent être définies afin de créer notre matrice de projection. Voici ces parties :

Plan near (proche) - c’est la distance au near plan de clipping à travers l’axe z négatif (dans espace de la caméra)
Plan far (lointain) - c’est la distance au far plan de clipping à travers l’axe z négatif (dans espace de la caméra)
Champ de vision (fov_y) - c’est l’angle entre les côtés en haut et en bas du frustum.
Le rapport d’aspect - c’est le rapport d’aspect de notre fenêtre.

La distance entre les plans near et far doit être aussi courte que possible pour minimiser le problème de précision du tampon de profondeur, ou, autrement dit, pour empêcher le z-fighting.

💡 Comment calculer la matrice de projection d’une caméra perspective

Faisons ce calcul en supposant que notre scène utilise une caméra perspective. Rappelons qu’il y a une différence entre la modélisation d’une caméra perspective et d’une caméra orthographique.

Avec gl-matrix, notre travail est très simple. On doit juste passer quelques paramètres à la méthode comme suit :

    const aspect = this._context.canvas.width / this._context.canvas.height;
    const projectionMatrix = mat4.create();
    const fov_y = (2 * Math.PI) / 5
    const near = 1
    const far = 100

    mat4.perspective(projectionMatrix, fov_y, aspect, near, far);

S’il y a une chance où vous auriez besoin de construire la matrice vous-même, ce ne sera pas trop mal :

\left[\begin{array}{cccc} { \dfrac{1}{(tan( fov_y / 2 ) * aspect)} } & 0 & 0 & 0 \\ 0 & { \dfrac{1}{ tan( fov_y / 2 )} } & 0 & 0 \\ 0 & 0 & -{\dfrac{f+n}{f-n}} & -{\dfrac{2fn}{f-n}}\\ 0 & 0 & -1 & 0\\ \end{array}\right]

Notez bien qu’il y a un -1 dans la position de la matrice [3][2] (en supposant que la matrice est indexée à 0) parce que la composante z (qui est négative) dans l’espace de vue devient notre composante w après avoir été multipliée par la matrice de projection :

\begin{pmatrix} x_{clip} \\ y_{clip} \\ z_{clip} \\ w_{clip} \end{pmatrix} = \begin{pmatrix} . & . & . & . \\ . & . & . & . \\ . & . & . & . \\ 0 & 0 & -1 & 0 \end{pmatrix} \begin{pmatrix} x_{view} \\ y_{view} \\ z_{view} \\ w_{view} \end{pmatrix}, \therefore w_{clip} = -z_{view}

💡 NB. Veuillez vous référer à cette illustration et notez la différence de direction de l’axe z dans l’espace de la caméra et dans l’espace de découpage. Spoiler : le système de coordonnées droitier devient gaucher.*

Gardons ce modèle de perspective dans notre poche arrière pendant que nous continuons l’histoire de la transformation des sommets à travers deux espaces qui jouent un rôle important pendant le pipeline de rendu - espace de découpage et NDC (coordonnées normalisées).

Mais avant d’y aller, nous avons encore un arrêt… coordonnées homogènes.

Les coordonnées homogènes.

Ah, les coordonnées homogènes m’ont fait peur il y a une semaine. J’ai vite compris qu’ils sont tout sauf effrayants. Ils sont en fait super utiles à avoir dans notre boîte à outils 3D.

Alors, pour commencer notre discussion, prenons l’exemple d’un sommet qui est positionné dans notre triangle d’il y a deux semaines comme suit :

(x, y, z, w) = (-1.0, -1.0, 0, 1)

Pourquoi est-ce qu’il y a quatre dimensions ? La position de ce sommet est considérée comme une coordonnée homogène parce qu’il y a une quatrième composante, w. Nous travaillons donc avec eux depuis le début !

On a besoin de cette quatrième dimension pour quelques raisons. On verra comment on les utilise, mais aussi comment le GPU les utilise (pour changer de l’espace de découpage à NDC) dans la prochaine partie.

Les applications

Il y a plusieurs applications qui nous seront immédiatement utiles. Note bien que cette liste que je dresse n’est pas entièrement complète. L’application de coordonnées homogènes est vaste !

La transformation projection

On utilise les coordonnées homogènes afin de travailler dans l’espace projectif.

Prenons un exemple 2D pour simplifier le concept :

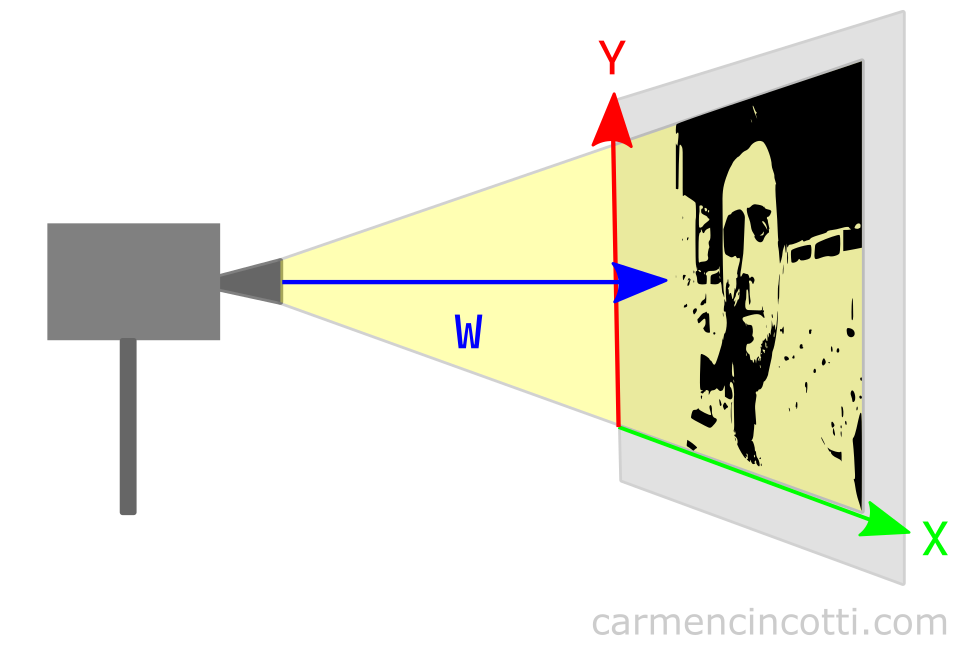
Illustration montrant une caméra projetant sur un écran avec des étiquettes pour W, X et Y

En regardant l’illustration, on peut voir que w a quelque chose à voir avec la projection. Imaginons que l’on rapproche le projecteur de cinéma de l’écran (qui affiche ma tronche).

L’image devrait rétrécir ! D’ailleurs, si l’on éloigne le projecteur de film de l’écran, l’image devrait grossir ! On peut donc en déduire que la composante w affecte l’échelle de l’image par rapport à la projection.

On verra plus tard comment cette valeur est utilisée par notre GPU pour rendre l’image avec une illusion de perspective correcte.

💡 Est-ce que w = 1 tout le temps ?

Je pense que la première question à se poser est : w = 1, qu’est-ce que cela veut dire ?

Comme on vient de le voir, la valeur w décrit l’échelle de nos composantes par rapport à la distance de la projection. Une valeur de 1 signifie donc qu’aucune mise à l’échelle ne se produit. Ainsi, lorsque w = 1, elle n’a aucun effet sur les valeurs des composantes x, y ou z.

Ainsi, définir w = 1 est une valeur initiale très raisonnable. Dans le code, lorsque nous définissons nos sommets, nous définissons la valeur sur 1, ce qui délègue essentiellement la responsabilité de la mise à jour de cette composante à la matrice de projection.

Ainsi, une fois tous les calculs terminés, w ne sera probablement plus égal à 1.

La translation des coordonnées 3D

Cette application est largement utilisée partout dans le monde graphique. En fait, on l’a déjà vue il y a une semaine avec nos matrices 4D lookAt et viewMatrix.

Habituellement, le vecteur de translation s’écrit sous forme de vecteur 3D et qui est considérée comme une transformation affine. En plus, les matrices de rotation et de mise à l’échelle sont également 3D (3x3) :

translation = [1, 1, 0] \\ rotation = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \\ scale = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}

Est-ce possible de représenter une transformation entière (translation, rotation, échelle) dans une seule matrice ? Oui ! En ajoutant le 4e composante, w, nous exploitons la puissance de la 4e dimension :

translation = [1, 1, 0, 1] \\ rotation = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \\ scale = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \\ T = t * S * R

Dès que l’on ajoute cette quatrième dimension, nous pouvons alors multiplier ces matrices pour construire une seule matrice :

T = t * S * R

Où $T$ est la matrice de transformation finale dans la forme 4x4. C’est exactement la même forme de notre matrice viewMatrix de la semaine dernière :

viewMatrix = \begin{bmatrix} R_x & U_x & F_x & 0 \\ R_y & U_y & F_y & 0 \\ R_z & U_z & F_z & 0 \\ -t_x & -t_y & -t_z & 1 \\ \end{bmatrix}

_{^{💡 Pour en savoir plus, une bonne ressource que je vous recommande de regarder est de la chaine YouTube de Keenan Crane.}}

L’espace de découpage

L’espace de découpage - Qu’est-ce que ? Je pense que cette illustration peut nous aider à l’éclairer :

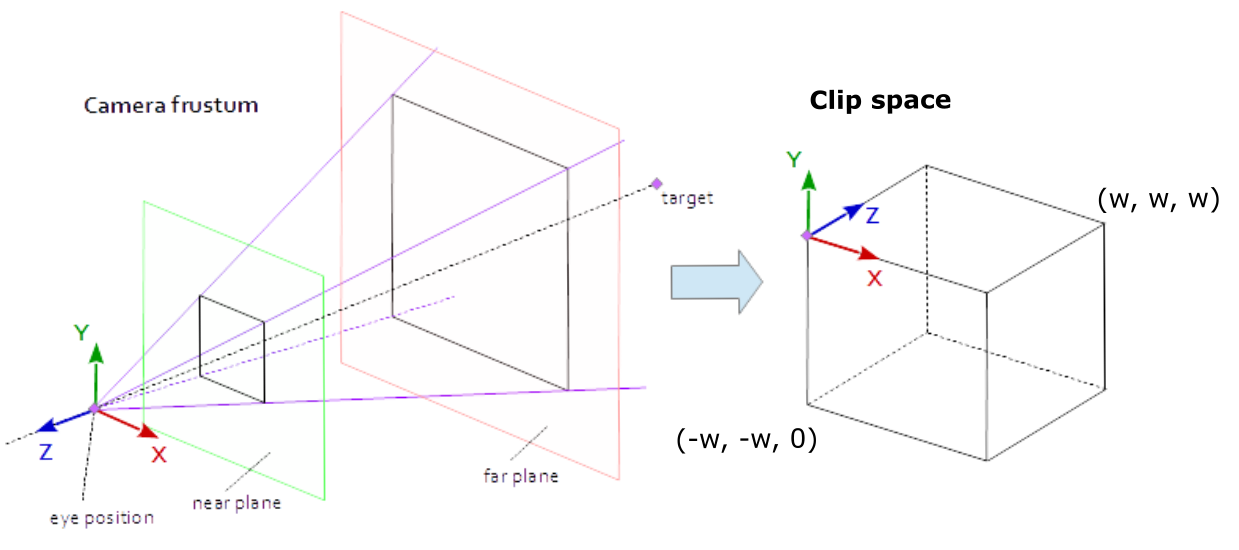
Projection view frustum into Clip space

Bref, l’espace de découpage est modélisé comme un prisme, qui s’appelle le volume découpage. S’il y a des sommets d’une primitive qui sont en dehors de cet espace, ils seront rejetés (coupés) par notre GPU. Il le fait afin d’éviter des calculs inutiles puisque nous ne pouvons pas voir ces sommets, de toute façon.

Les dimensions du volume de découpage sont définies comme la boîte englobante suivante : $(-w, -w, 0), (w, w, w)$ où $w$ est la dimension supplémentaire du sommet, ce qui fait du sommet une coordonnée homogène !

Afin d’éviter d’être rejetés par notre GPU, les composantes x, y, et z d’un sommet dans l’espace de découpage doivent remplir ces conditions :

−w ≤ x ≤ w \\ −w ≤ y ≤ w \\ 0 ≤ z ≤ w

Comment entrer l’espace de découpage

Nos sommets sont positionnés dans l’espace de découpage par nous.

Comment ? Les calculs impliqués dans la transformation de notre sommet positionné dans l’espace modèle en espace de découpage se produisent dans le shader de vertex. En fait, la position que nous définissons en sortie est la position dans l’espace de découpage.

L’équation généralement utilisée dans un shader de vertex est la suivante :

out.position = projectionMatrix * viewMatrix * modelMatrix * inputPosition

où :

inputPosition - la position du sommet 4D (coordonnée homogène) dans l’espace modèle.
modelMatrix - la matrice 4x4 qui transforme les sommets d’entrée de l’espace modèle à l’espace monde.
viewMatrix - la matrice de vue 4x4, qui prend en entrée un point dans l’espace du monde et le résultat est un point dans l’espace de la caméra.
projectionMatrix - la matrice de projection 4x4, qui prend en entrée un point dans l’espace de la caméra et le résultat est un point projeté dans l’espace de découpage.

Ce qui est un peu déroutant pour moi, c’est le fait que chaque sommet peut avoir une valeur w_c différente. On devrait donc considérer l’espace de découpage comme un prisme rectangulaire et que chaque sommet a son propre espace de découpage dans lequel il existe..

💡 Et le triangle qui a des sommets à l’intérieur et à l’extérieur du volume de découpage ?

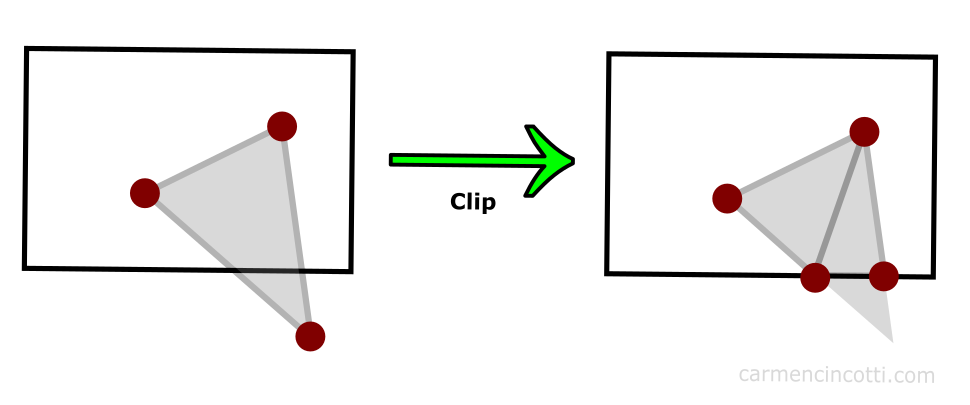
A triangle being clipped

Notre GPU est très malin. À l’aide d’un algorithme (que je n’aborderai pas en profondeur dans cet article), les sommets qui se trouvent en dehors de l’espace de découpage sont coupés, et à leur place, le GPU redessine d’autres sommets :

Le résultat est une primitive coupée, mais toujours présente dans la scène. Ces nouveaux sommets peuvent créer les triangles supplémentaires si le GPU le juge nécessaire.

NDC

Après avoir supprimé les sommets qui tombaient à l’extérieur du volume de découpage, les positions de tous les sommets restants sont normalisées dans un système de coordonnées commun appelé NDC (Coordonnées de l’appareil de normalisation).

Transformation from view space to NDC

Le GPU fait du travail pour entre dans ce système de coordonnées en faisant une opération appelée division de perspective où toutes les composantes du sommet sont divisées par la composante w.

{\begin{pmatrix}x_{ndc}\\y_{ndc}\\z_{ndc}\end{pmatrix}}={\begin{pmatrix}{\tfrac {x_{c}}{w_{c}}}\\{\tfrac {y_{c}}{w_{c}}}\\{\tfrac {z_{c}}{w_{c}}}\end{pmatrix}}

Rappelez-vous qu’on vient de découper tous les sommets qui se trouvaient en dehors du prisme de dimensions w. Nos composantes doivent donc se situer entre -1 et 1 après les avoir normalisés en divisant les composantes x et y par la composante w. Pour la composante z, les coordonnées normalisées tomberont entre 0 et 1.

⚠️ Chaque API graphique est différent et il faut que vous voyiez les docs de l’API graphique que vous utilisez, mais dans le cas de WebGPU, NDC est comprise entre (-1, -1, 0) et (1, 1, 1).

La suite

Nous continuons cette histoire en voyant comment nous arrivons à l’espace d’écran 2D de NDC !

Carmen's Graphics Blog