Cette semaine, je voudrais continuer la discussion sur le pipeline de rendu graphique. La semaine dernière, on a abordé la discussion sur la transformation d’un sommet à partir de 3D en 2D.
Vous vous demandez peut-être :
Comment transformer ces sommets en pixels ?
Pour répondre, nous allons parler du processus de la rastérisation.
Rastérisation
La rastérisation est le processus par lequel le GPU trouve tous les pixels à l’intérieur d’une primitive (le GPU ne rastérisera que les triangles) en utilisant les sommets transformés de la primitive donnée (chacun avec une valeur z, et d’autres informations qui lui sont associées).
Voici un GIF qui nous montre une illustration de haut niveau de la rastérisation :
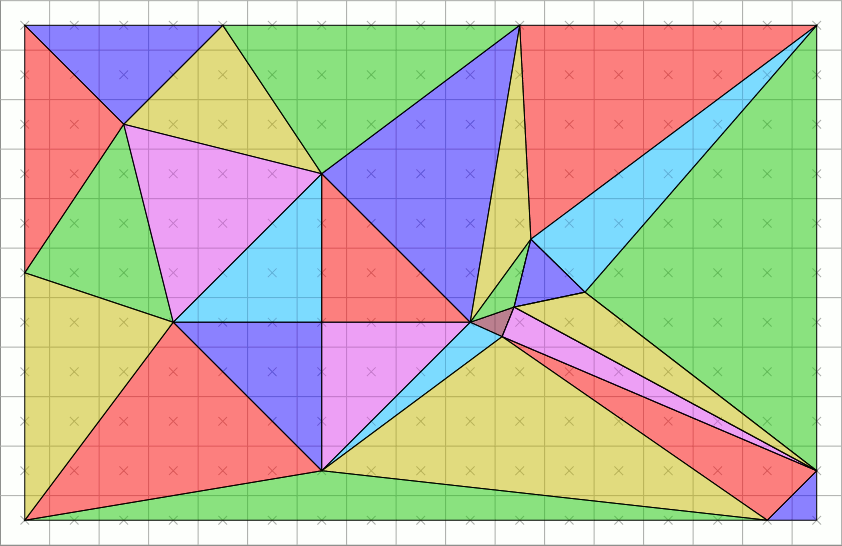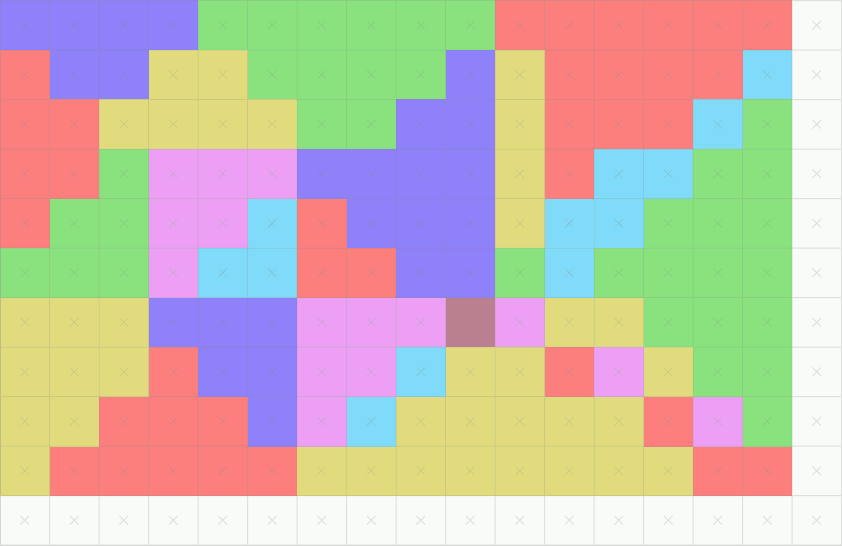
Nous voyons comment les primitives (triangles) se transforment en pixels. Autrement dit, les triangles sont rastérisés en pixels.
On verra bientôt que ce processus n’est pas si simple si nous voulons une belle image rendue (à cause du crénelage (aliasing)), mais la rastérisation elle-même est assez facile à comprendre, comme on le verra.
Cela étant dit, notre première étape consiste à apprendre comment le GPU détermine si un pixel se trouve ou non dans un triangle donné.
💡Pourquoi le GPU n’utilise-t-il que des triangles lors de la rastérisation ?
En plus d’être le primitif le plus simple (après une droite et un sommet), il y a deux raisons importantes pour lesquelles l’utilisation de triangles est avantageuse :
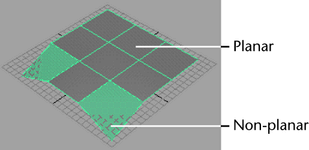
- La complexité - les triangles sont très moins complexes par rapport aux autres primitives d’ordre supérieur. Un triangle ne peut jamais être non-planaire.
Autrement dit, tous les sommets d’un triangle existent dans le même plan :
- L’efficacité - comme les triangles sont moins complexes, les algorithmes pour les rendre sont très rapides. En plus, les triangles nécessitent moins de ressources (mémoire) pour les rendre.
La couverture en pixels d’un triangle
Je vais couvrir ce sujet de manière générale. Le trou dans lequel nous pouvons tomber est profond.
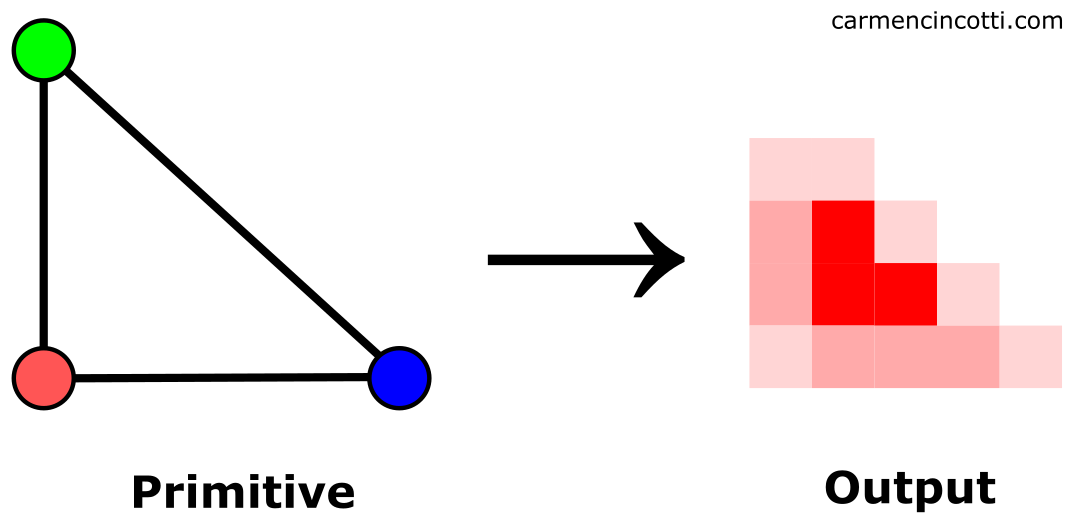
Cela dit, je vais commencer par notre première étape : assembler des triangles à partir de sommets.
La mise en place d’un triangle (assemblage primitif)
La première étape lors du processus de la rastérisation consiste à assembler tous les sommets encore visibles après le processus de clipping.
Au cours de cette étape, les équations de bord (edge equations), les équations différentielles (differential equations), et d’autres informations sur les triangles sont calculées.
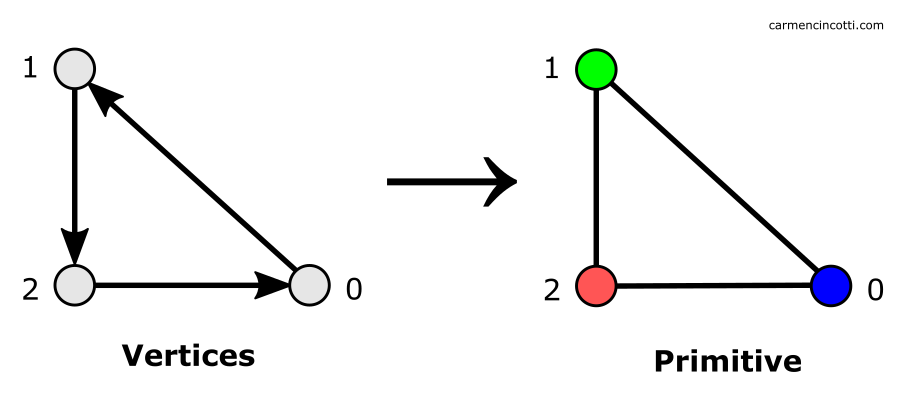
La traversée d’un triangle
Après avoir calculé les informations nécessaires pour déterminer les bords d’un triangle, la prochaine étape consiste à traverser les pixels de l’écran afin de trouver ceux qui sont à l’intérieur d’un triangle donné.
Le GPU les utilisera pour déterminer si un pixel (ou plutôt, comme on le verra - un échantillon) est à l’intérieur ou non en exécutant un test de couverture (coverage test).
💡 Il y a des optimisations pour éviter de traverser tous les pixels sur un écran. Par exemple, le GPU peut limiter cette traversée à une boîte englobante (bounding box) qui entoure un triangle donné.
Première approche - un seul échantillon pour chaque pixel
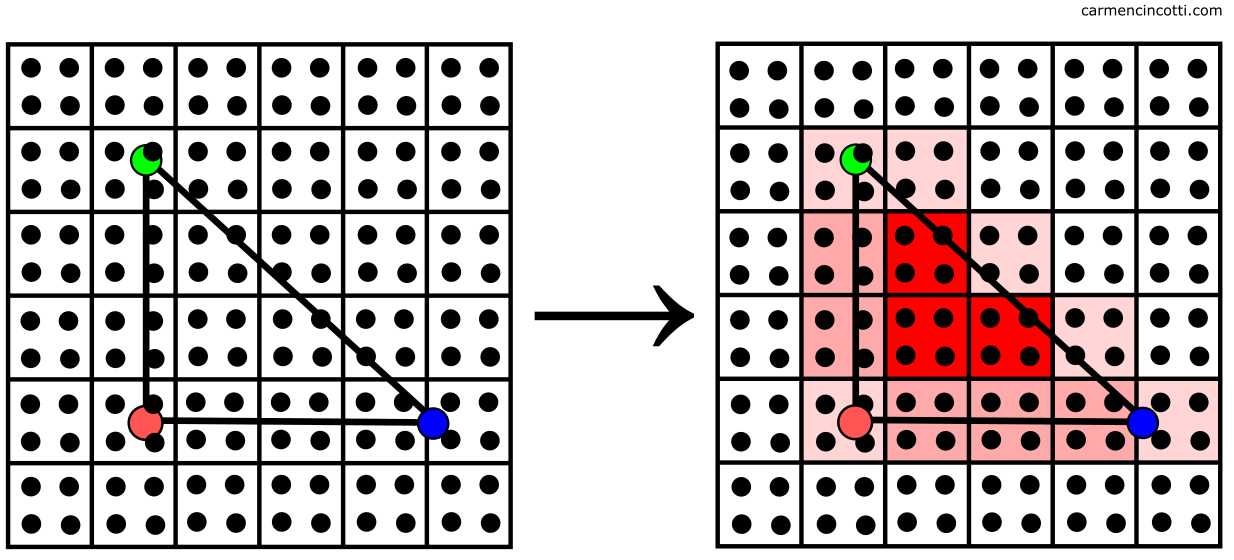
Pour commencer, une approche naïve consiste à déterminer si le centre d’un pixel se trouve à l’intérieur d’un triangle :
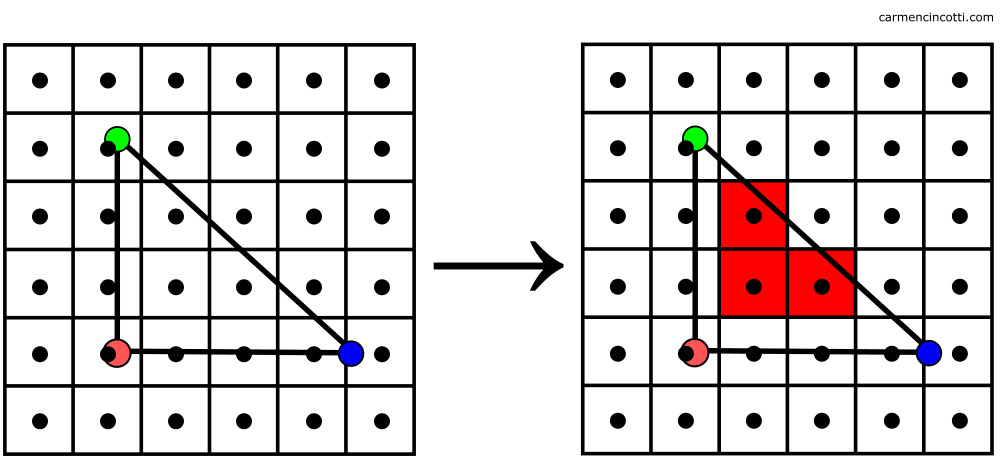
La grille située à gauche nous montre les pixels de sortie et les points représentent le centre de chacun. À droite, on voit les pixels mis en avant dont ses centres sont à l’intérieur du triangle.
Mais, comme vous l’avez probablement déjà remarqué - il y aura des erreurs d’approximation. Notre image sera mal rendue :
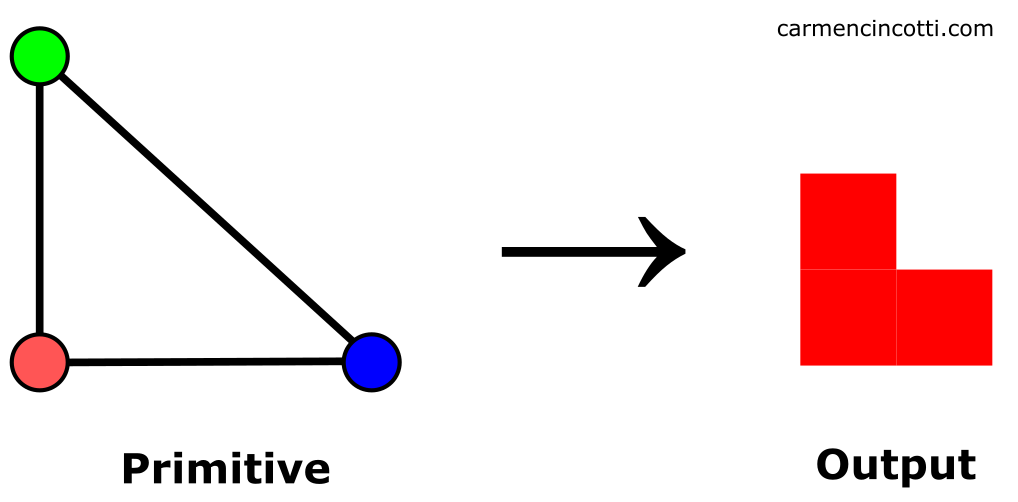
🎉 Félicitations 🎉 ! On vient de voir un problème très connu dans le monde de l’infographie - le crénelage (aliasing). Il est dû à un échantillonnage (sampling) insuffisant. Explorons ces sujets d’un peu plus près.
L’échantillonnage
L’échantillonnage est le processus de réduction d’un signal à temps continu en un signal à temps discret. Le but est de représenter numériquement des informations continues données aussi précisément que possibles.
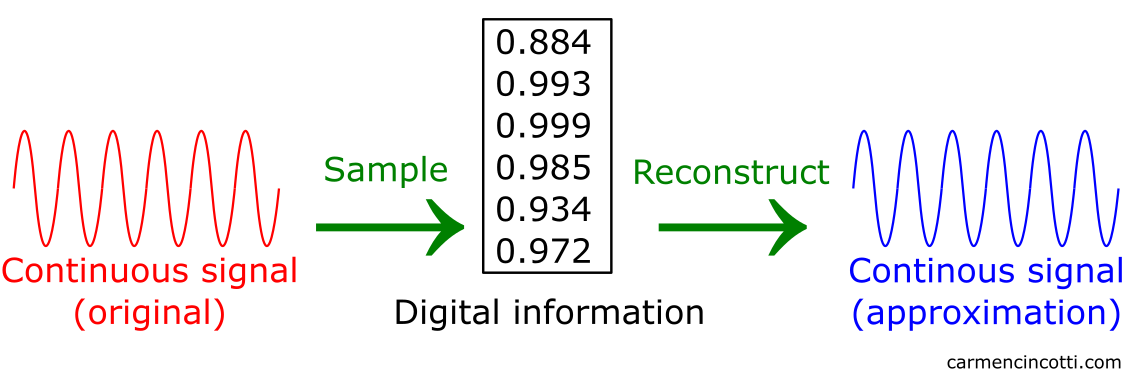
Après avoir prélevé des échantillons, nous pouvons prendre ces informations numériques pour approximer et récupérer le signal continu d’origine. Ce signal approximatif est appelé une reconstruction. Un filtre est utilisé lors de ce processus de reconstruction afin de réobtenir un signal continu approximatif.
Bref, nos primitives sont comme des signaux continus. Nous aimerions les dessiner sur des pixels - une structure discrète.
Par conséquent, il faut échantillonner nos primitives pour obtenir les informations numériques nécessaires pour les reconstruire en pixels colorés sur notre écran. Revoyons cette image :

Comme on l’a déjà vu : le centre de chaque pixel représente un échantillon (sample) - un emplacement discret à l’intérieur d’un pixel. Nous pouvons facilement rendre compte que les bords de l’image de sortie ne se conforment pas au triangle d’origine.
Ce problème nous montre les contraintes imposées par les pixels que nous devons prendre en compte.
Quelles sont les contraintes imposées ?
Les contraintes sont les suivantes :
- Couleur - Un pixel donné ne peut être qu’une seule couleur.
- Tout ou rien - Un pixel est entièrement coloré par cette couleur choisie. Il est impossible de colorer juste une petite partie d’un pixel.
Voici un exemple clair de ce drapeau pixelisé :
![]()
Chaque pixel de l’image du drapeau rastérisé est coloré d’une seule couleur (rouge ou blanc), et entièrement coloré avec cette couleur.
Combien d’échantillons que faut-il prélever pour obtenir la meilleure image possible ?
La réponse est probablement mieux expliquée dans le contexte de crénelage.
⚠️Il faut dire que nous devrons seulement nous intéresser à cette idée de ce qu’est un échantillon, et pas à la façon dont ils sont colorés. Cela sera expliqué dans un prochain article.
Le crénelage (aliasing).
Problème 🤔 : les signaux récupérés ne sont jamais parfaitement précis.
Eh bien, pouvons-nous au moins être proches de la perfection ?
La fréquence d’échantillonnage joue un rôle principal dans ce cas. Cependant, il nous faut choisir une fréquence qui est à la fois suffisante pour récupérer avec précision un signal donné sans épuiser toutes nos ressources hardwares.
Ceci dit, le sous-échantillonnage peut modifier considérablement le signal récupéré final. Les artefacts de rendu causés par ces erreurs du sous-échantillonnage s’appellent le crénelage (aliasing).
Voilà une animation qui nous montre comment le sous-échantillonnage d’un signal peut effectivement rendre inutile le signal reconstruit. Le signal source est noir, et le signal récupéré est en rouge. Les points sur la ligne rouge sont des points où on prélève les échantillons :

Évaluons les fréquences d’échantillonnage que nous avons vues au cours de ce GIF :
✅ Au début : On voit une fréquence d’échantillonnage suffisante pour reconstituer le signal source.
🆗 Au milieu : La fréquence d’échantillonnage diminue, mais nous ne perdons pas trop d’informations. Nous pouvons toujours être sûrs que notre reconstruction de notre signal source est correcte.
💥 À la fin : Le scénario catastrophe a été atteint. Le taux d’échantillonnage est si bas que le signal récupéré est complètement méconnaissable à sa source.
Sachant cela, précisons notre définition du crénelage :
Le crénelage - lorsque les hautes fréquences d’un signal d’origine font semblant d’être des basses fréquences après avoir été reconstruites en raison d’un sous-échantillonnage.
Voyons comment nous pouvons empêcher ce phénomène.
L’anticrénelage - super-échantillonnage
Si nos images souffrent de crénelage, il nous faut augmenter la fréquence d’échantillonnage !.
Le GPU peut échantillonner un pixel à plusieurs reprises par un processus qui s’appelle le super-échantillonnage. Regarde cette image où le carré est un pixel dont le centre est représenté par une croix :

Dans ce cas, nous pouvons échantillonner chaque pixel à quatre reprises (les points bleus) !
Ensuite, une valeur de couleur moyenne est calculée en utilisant les pixels supplémentaires pour le calcul.
Le résultat est une image avec des transitions de pixel à pixel plus fluides le long des bords des triangles comme suit :
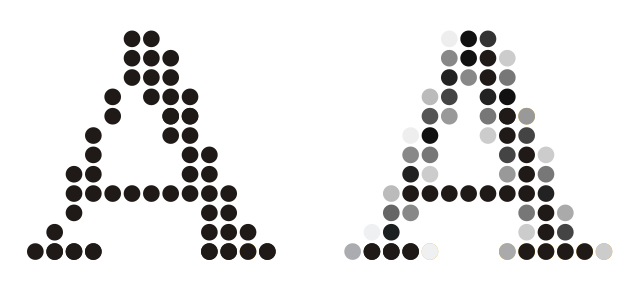
🎉 Enfin 🎉, nous sommes prêts à ressayer de rastériser notre image.
💡*Il existe plusieurs méthodes de super-échantillonnage*
⚠️Il faut dire que le super-échantillonnage exigera plus de ressources matérielles et de temps pour rendre une image.
Deuxième approche - plusieurs échantillons pour chaque pixel
En prenant plusieurs échantillons et en calculant une valeur de couleur moyenne, le GPU est capable de rastériser la primitive comme suit :
Et enfin, on voit cette image bien plus belle :
En échantillonnant plus de fois, nous sommes capables de rastériser une primitive qui est beaucoup plus fidèle à la primitive source que notre précédente tentative “un échantillon par pixel”.
La suite
Je pense que la prochaine étape consiste à comprendre les fragments - ce qu’ils sont et comment ils sont traités. À bientôt !
Des ressources (en français et anglais)
- Computer Graphics (CMU 15-462/662) - Keenan Crane
- Real-Time Rendering, Fourth Edition, by Tomas Akenine-Möller, Eric Haines, Naty Hoffman, Angelo Pesce, Michał Iwanicki, and Sébastien Hillaire
- Rasterization: a Practical Implementation - Scrathapixel
- Supersampling - Wikipédia
- Rasterization and sampling - Imperial College London
- Serious Statistics: The Aliasing Adventure - Overclockers Club
- Intro to Graphics Rendering - Jason L. McKesson
- A Stackoverflow question I found helpful
