L’éclairage d’une scène 3D est nécessaire pour donner une impression de réalisme. Dans la vraie vie, la lumière est partout. Par exemple, nous trouvons du soleil à l’extérieur. Il y a de la lumière des lampes sur nos bureaux. Les lampadaires nous guident la nuit, etc.
L’autre côté de l’éclairage, c’est des matériaux qui le reçoivent. La façon dont la lumière interagit avec un matériau dépend de ses propriétés de surface. Est-ce que le matériau brillant ? Rugueux ? Terne ?
En appliquant de l’éclairage dans une scène 3D, nous pouvons introduire du réalisme dans nos scènes. En outre, nous pouvons voir plus de détails sur nos modèles. Voici la face arrière du lapin sans un modèle d’éclairage 🐇 :

Voici le résultat du lapin avec un tel modèle :

La différence est claire et brillante ! Un modèle typique et basique avec lequel nous éclairons nos scènes s’appelle le modèle d’éclairage Phong.
Le modèle d’éclairage Phong 💡
Le modèle se compose de trois parties :

Par Brad Smith; — Travail personnel, CC BY-SA 3.0, Lien
Ces trois parties sont :
- Ambient - Le monde n’est jamais parfaitement sombre, car il y a de la lumière qui peut provenir d’un cumul de sources insignifiantes (lumières d’une ville lointaine, la lune dans une nuit étoilée, etc.). Il est beaucoup plus facile de modéliser cela comme une valeur constante pour éviter des calculs complexes.
- Diffuse - Cet éclairage dépend de la position et de la direction de la source lumineuse. Si la surface d’un objet fait directement face à la source lumineuse, elle serait plus brillante que dans le cas contraire.
- Spéculaire (specular) - Le repère brillant sur l’objet sous une lumière. L’ampleur de cet effet dépend du matériau de l’objet et la position de la caméra.
Ce modèle n’est que cela - un modèle. D’autres modèles existent. Cependant, pour créer une scène performante et jolie à la fois, il faudra prendre des raccourcis !
L’éclairage ambiant
L’éclairage ambiant est une composante simple de l’éclairage d’une scène. C’est une source de lumière qui éclaire un objet uniformément.
Pour autant, cette approximation ‘éclairement uniforme’ est une grosse simplification du comportement des photons. Les photons de n’importe quelle source rebondissent et se dispersent.

Si nous supposons dans la vraie vie qu’il existe de nombreuses sources de lumière, nous devrions totalement éviter le calcul super complexe en approximant le comportement des photons en ajoutant juste une couleur constante à l’image finale.
Voici un exemple de cube avec un éclairage ambiant appliqué :

On ajoute le code d’éclairage ambiant dans le shader de fragment comme suit :
@stage(fragment)
fn main(fragData: VertexOut) -> @location(0) vec4<f32>
{
let ambientLightIntensity = 0.2;
let lightFinal = ambientLightIntensity;
return vec4(1.0, 1.0, 0., 1.0) * lightFinal;
}
L’éclairage diffus
Dans la vraie vie, un objet n’est jamais éclairé de manière homogène. Par exemple, une face d’un objet sous une lampe, du soleil, etc. serait plus brillante si elle se trouve directement sous la lumière. En revanche, une face faisant face à la direction opposée serait plus sombre.
Une propriété d’un matériau, c’est sa capacité à refléter et à disperser la lumière. L’éclairage diffus se caractérise par le comportement observé lorsqu’une surface reflète et disperse la lumière dans tous les sens :

Nous pouvons facilement simuler ce comportement en utilisant l’algèbre linéaire. Si vous ne comprenez rien de l’algèbre linéaire, ce n’est pas grave ! Regardez cette image qui représente le modèle diffus que nous allons simuler :

Imaginez que la face de l’objet soit le mur de briques avec un vecteur normal (en rouge) pointant vers le haut. Un angle se forme entre la source de lumineuse et le vecteur normal qui s’appelle l’angle d’incidence.
Vecteur normal
Un vecteur normal est un vecteur unitaire qui est perpendiculaire à la surface à un sommet donné.

Rappelez que nous avons utilisé Blender pour exporter nos fichiers .OBJ. Les normales sont donc déjà définies pour nous. Il est toujours possible de les calculer avec le produit vectoriel.
L’implémentation d’éclairage diffus
Voici le code du shader de sommet :
@stage(vertex)
fn ${VERTEX_ENTRY_POINT}(
@location(0) position: vec4<f32>,
@location(1) normal: vec4<f32>) -> VertexOut
{
var output : VertexOut;
output.position = projectionMatrix * viewMatrix * modelMatrix * position;
output.vNormal = normalMatrix * normal;
output.vPos = modelMatrix * position;
return output;
}
Pour calculer la magnitude de la lumière diffuse, nous avons besoin de vNormal et de vPos. Ce choix de multiplier la position par le modelMatrix sera plus clair une fois que nous aurons introduit le code shader de fragment dans la section suivante.
Ce qui m’intéresse, c’est l’idée d’introduire le concept d’une soi-disant normalMatrix. Je vais prendre un sidebar pour en parler.
La matrice normale
La matrice normale est une matrice de transformation que nous utilisons afin de transformer les normales d’un objet. Il est vraiment important de les utiliser dans le cadre de calculs de lumière.
Examinons d’abord le problème que les matrices normales résolvent.

Si je fais tourner un cube, les normales resteront les mêmes, car nous ne transformons que les positions des sommets (avec le modelMatrix dans le shader de vertex), et pas les normales (comme on le voit avec le cube de gauche). Cependant, pour calculer la relation entre le vecteur normal et la lumière, les normales doivent tourner avec l’objet (cube de droite). Cela se fait en transformant nos valeurs normales avec la matrice normale !
Pourquoi faut-il utiliser une telle matrice, et ne pas prendre aveuglément l’inverse de la matrice modèle ?
Il est possible de le faire, mais le problème avec la matrice modèle, c’est qu’une telle matrice peut avoir une mise à l’échelle de manière non uniforme - ce qui changerait totalement la direction du vecteur normal après l’avoir calculé.
Comment calcule-t-on une telle matrice ?
Le pseudocode est comme suit :
transpose(invert(modelMatrix))
Encore une fois, je peux utiliser la modelMatrix s’il n’y a pas de mise à l’échelle de manière non uniforme. Pour en savoir plus, je vous recommande cet article.
Voilà le code du shader de fragment :
@stage(fragment)
fn ${FRAGMENT_ENTRY_POINT}(fragData: VertexOut) -> @location(0) vec4<f32>
{
let diffuseLightStrength = 1.4;
let ambientLightIntensity = 0.2;
let vNormal = normalize(fragData.vNormal.xyz);
let vPosition = fragData.vPos.xyz;
let lightPosition = lightModelPosition.xyz;
let lightDir = normalize(lightPosition - vPosition);
let lightMagnitude = dot(vNormal, lightDir);
let diffuseLightFinal: f32 = diffuseLightStrength * max(lightMagnitude, 0);
let lightFinal = diffuseLightFinal + ambientLightIntensity;
return vec4(1.0, 1.0, 0., 1.0) * lightFinal;
}
Ce qui m’intéresse, c’est le calcul du lightDir et lightMagnitude.
La direction de la lumière
Prenons un exemple pour clarifier ce calcul :
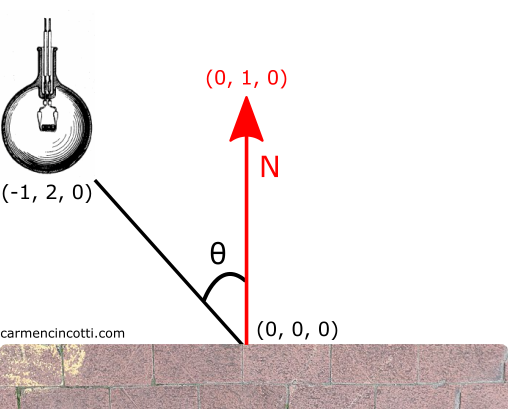
Au début, nous devons faire le calcul pour lightDir, qui est le vecteur directeur vers laquelle la source de lumière pointe.
Supposons que la position de la lumière soit à (-1, 2, 0) et que la position de la surface soit à (0, 0, 0). Le calcul pour lightDir est le suivant :
💡 Nous devons la normaliser parce que c’est une direction. Cette normalisation sera également utile lors du calcul de la magnitude de la lumière, lightMagnitude, qui dépend du produit scalaire.
La magnitude de la lumière
On utilise le produit scalaire pour déterminer dans quelle mesure lightDir est projeté sur le vecteur normal (pointant vers (0, 1, 0)). Ce calcul nous rendre une valeur scalaire qui peut être utilisée pour mettre à l’échelle la contribution de la lumière diffuse à l’image finale.
Voilà ! Il faut contribuer 89.44% de la lumière diffusée à la couleur de ce fragment.
Le résultat de l’implémentation
Pour conclure la discussion de la lumière diffuse, je voudrais montrer des résultats :

L’éclairage spéculaire
L’éclairage spéculaire est associé à une certaine brillance d’un matériau réfléchissant.

Regardons ce violon. En son milieu, il y a des reflets lumineux. Ce comportement est modélisé par le modèle de réflectance spéculaire qui se ressemble à un miroir :

L’éclairage spéculaire implémentation
Nous devons trouver le vecteur réflexion qui est le reflet de la direction de la lumière autour du vecteur normal, puis calculer l’angle d’incidence entre ce vecteur et la direction de la caméra.

Voici du code :
let specularStrength = 0.5;
let specularShininess = 40.;
let vNormal = normalize(fragData.vNormal.xyz);
let vPosition = fragData.vPos.xyz;
let vCameraPosition = cameraPosition;
let lightDir = normalize(lightPosition - vPosition);
let lightMagnitude = dot(vNormal, lightDir);
let diffuseLightFinal: f32 = diffuseLightStrength * max(lightMagnitude, 0);
let viewDir = normalize(vCameraPosition - vPosition);
let reflectDir = reflect(-lightDir, vNormal);
let spec = pow(max(dot(viewDir, reflectDir), 0.0), specularShininess);
let specularFinal = specularStrength * spec;
let lightFinal = specularFinal;
return vec4(1.0, 1.0, 0., 1.0) * lightFinal;
J’ai inclus quelques paramètres pour modifier la puissance de la brillance avec specularShininess. C’est à vous de jouer avec ce paramètre !
Et enfin - voici le résultat du cube avec tous les trois modèles d’éclairage appliqués :

Des exercices
Un exercice potentiel serait d’écrire le shader de fragment de sorte qu’il inclue les trois effets d’éclairage dans le modèle de Phong !
