Dynamique basée sur la position | PBD

Nous sommes enfin prêts à commencer la simulation. Grâce à mes recherches, je suis tombé sur une façon super performante et passionnante de simuler le tissu -grâce à la puissance de la dynamique basée sur la position.

Keywords: simulation de tissu, méthodes numériques

By Carmen Cincotti

July 11, 2022Updated September 12, 2022

Avantages et inconvénients
L’algorithme
Des ressources (en français et anglais)

Pendant l’article où nous avons créé un système de particules hookéen, nous avons utilisé des forces externes et internes cumulées à partir desquelles les accélérations sont calculées sur la base de la deuxième loi de Newton pour simuler des effets physiques tels que l’étirement, le cisaillement et la flexion.

Cependant, il existe une méthodologie quasi nouvelle qui supprime les couches de vitesse et d’accélération, qui s’appelle la dynamique basée sur la position.

PBD demonstration

Source : Position Based Dynamics - Matthias Müller-Fischer, YouTube

Cette méthode nous permettra de résoudre notre système en travaillant directement sur les positions des particules en satisfaisant des fonctions contraintes.

Avec cette méthodologie, nous pouvons simuler du tissu aussi que des fluides, des déformations, etc. !

Avantages et inconvénients

Pour commencer, je voudrais souligner les avantages et les inconvénients par rapport aux simulations basées sur des forces externes et internes.

Avantages :
- Rapide, facile à mettre en place et contrôlable.
- Il évite les problèmes de “overshooting” rencontrés lors de l’utilisation de l’intégration temporelle explicite.
- Il est capable de fonctionner avec des contraintes arbitraires tant que le gradient de la fonction de contrainte peut être déterminé.
Inconvénients :
- La raideur du modèle dépend du paramètre de raideur ainsi que de l’ampleur du pas de temps et du nombre d’itérations du solveur.

L’algorithme

for all vertices i 
    initialize xᵢ = xᵢ_₀, vᵢ = vᵢ_₀, wᵢ = 1/mᵢ
while simulating
    for all particles 𝑖 (pre-solve)
        𝐯ᵢ ← 𝐯ᵢ + ∆𝑡*wᵢfₑₓₜ(𝐱ᵢ)
        𝐩ᵢ ← 𝐱ᵢ + ∆𝑡*𝐯ᵢ
    for solverIterationCount
        for all constraints 𝐶 (solve)
            solve(𝐶, ∆𝑡) (solve for 𝐱ᵢ)
    for all particles 𝑖 (post-solve)
        𝐱ᵢ ← 𝐱ᵢ + ∆𝐱ᵢ
        𝐯ᵢ ← (𝐱ᵢ − 𝐩ᵢ)/∆t

Source

Naviguons ensemble de ce pseudo-code pour mieux le comprendre. Supposons que nous utilisions une particule qui est contrainte à un fil, comme ce que vous pourriez voir sur un ‘bead rollercoaster’ (montagnes russes à perles en bois).

Initialisation

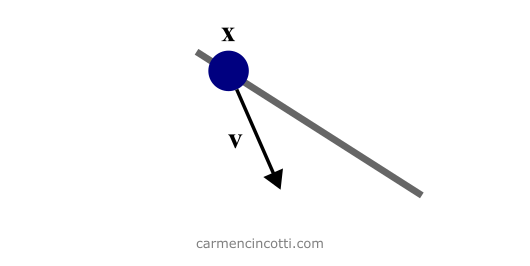
Initialization of the particle

Pour démarrer la simulation, nous devons initialiser nos attributs. Chaque particule a trois attributs : sa masse (m), sa position(𝐱) et sa vitesse (𝐯).

Imaginons à partir de ce scénario qu’il y a deux vitesses contributives - la vitesse de la gravité et une vitesse initialisée dans le sens du fil - qui donnent un vecteur de vitesse finale dans le sens indiqué sur l’image.

Après les avoir initialisés, nous pouvons commencer à les mettre à jour dans les étapes suivantes.

Pre-solve (prérésoudre)

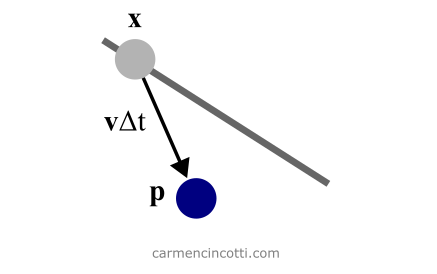
Particle is moved to new unconstrained position

Avant d’imposer les contraintes du fil, la particule se déplace vers le sens du vecteur vitesse pendant un intervalle de temps donné, Δt.

Pour ce faire, nous prenons un pas d’Euler. Nous avons déjà appris de cette méthode numérique il y a des mois.

Génial 🎉 ! Nous avons réussi à approximer la nouvelle position de la particule ! Cependant… elle n’est plus attachée au fil ! Réparons cela.

Solve (résoudre)

Move the particle back to the wire

En avant vers la beauté de la dynamique basée sur la position. Le solveur itératif manipule la position de la particule afin de satisfaire les contraintes.

Les contraintes

Il existe deux types de contrainte :

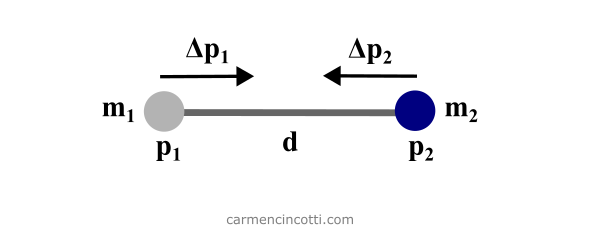
Égalité (bilatérale) - Les contraintes d’égalité sont des contraintes qui doivent toujours être appliquées. Un exemple de ce type de contrainte est une contrainte de distance où, disons, $d = 2$ :

Distance constraint example

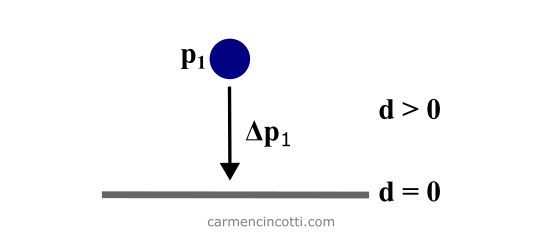
Inégalité (unilatérale) - Une contrainte d’inégalité utilise l’opérateur de comparaison $<=$ or $>=$ . Il existe donc plusieurs solutions qui peuvent satisfaire une telle contrainte. Par exemple, voici cette particule qui est en train de tomber au sol. Elle continuera à tomber tant que $d > 0$ :

Falling ball to ground example

En plus, un point important est que ces contraintes font partie à un groupe de contraintes considérées comme non linéaires. Voici la différence entre les contraintes non linéaires et linéaires :

Linéaire - Les contraintes d’inégalité linéaires ont la forme $A·x ≤ b$ . Les contraintes d’égalité linéaires ont la forme $A·x = b$ .
Non linéaire - Les contraintes d’inégalité non linéaires ont la forme $c(x) ≤ 0$ . De même, les contraintes d’égalité non linéaires ont également la forme $c(x) = 0$ .

La différence entre des systèmes linéaires et non linéaires est hors du cadre de cet article, mais on les redécouvrir peut-être bientôt !

Le solveur itératif

Comme je l’ai déjà dit, le travail du solveur est de déplacer la particule afin de satisfaire les contraintes.

Le problème à résoudre est un ensemble de $M$ équations pour les $3N$ composantes de position inconnue. Cependant, le nombre de contraintes $M$ n’est pas nécessairement égal à $3N$ . Dans ce cas, le système est considéré comme asymétrique.

Connaissant ces détails, nous pouvons considérer le système que nous devons résoudre comme un système asymétrique et non linéaire avec des égalités et des inégalités. Quelle horreur ! 👻

Le processus est itératif comme nous pouvons voir en voyant le boucle utilisant solverIterationCount. Également, chaque contrainte est résolue individuellement en utilisant un solveur Gauss-Seidel non linéaire.

Nous en verrons plus dans un article suivant. Pour l’instant, mon but est de présenter toutes ces connaissances de manière de haut niveau.

Post-solve (après avoir résolu)

Post solve step image

Après avoir satisfait les contraintes et ramené la particule sur le fil, nous devons résoudre la nouvelle vitesse. Enfin, la boucle est répétée !

Carmen's Graphics Blog