Carmen's Graphics Blog

Computer Graphics and Physics Simulation Tutorials and Articles
PostsAboutProjectsJobs

La contrainte de distance | XPBD

XPBD utilise des contraintes de particules pour s'assurer que les particules se déplacent d'une certaine manière, par rapport aux autres particules. Examinons de plus près une contrainte commune que nous trouverons dans une simulation de tissu, la contrainte de distance.

Keywords: dynamique basée sur la position, simulation de tissu, lagrange, physique, infographie

By Carmen Cincotti  

Une grande pièce du puzzle de XPBD, dont nous avons déjà parlé il y a quelques semaines, est la satisfaction des contraintes de particules. Les contraintes de particules forcent une particule à se déplacer et à agir d’une certaine manière, par rapport aux autres particules dans le système.

How a particle moves back to the string

Si vous me suiviez depuis quelques mois, vous connaissez sans doute mon objectif de simuler le tissu 🧵. Une telle simulation peut avoir des contraintes complexes, mais pour l’instant, nous ne considérerons que les contraintes de distance et les contraintes de flexion.

Voici ces fameux articles que nous avons déjà étudiés lors d’un article il y a quelques semaines sur XPBD que je vais référencer pour les maths au cours de ce post :

Un résumé de XPBD

Rappelons que l’algorithme de XPBD à petits pas est défini comme suit :

Algorithm of XPBD with small steps

⚠️ Comme je l’ai dit, nous avons déjà parlé de cet algorithme à fond et je vous recommande de lire l’article si vous êtes déjà perdu.

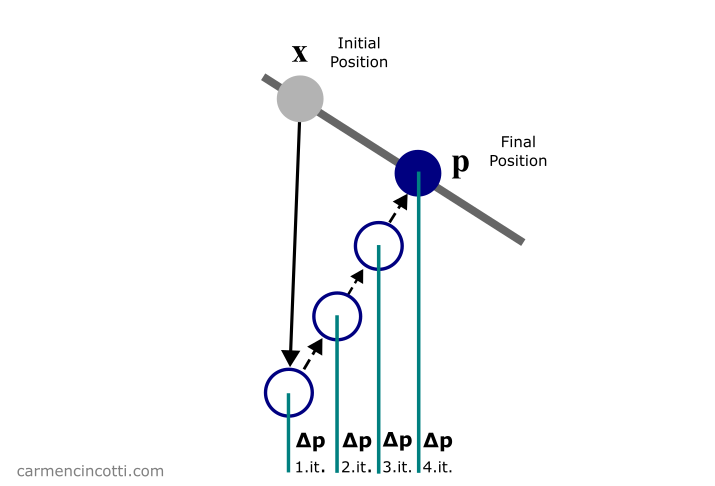
Pour l’instant, la boucle qui se trouve seule dans les lignes (6) - (11) nous intéresse. Comme vous pouvez le voir, la fonction de cette boucle est de satisfaire les contraintes de la simulation afin de corriger directement les positions de chaque particule qui participe aux contraintes.

On vient de couvrir la raison pour laquelle cette méthode de simulation s’appelle la dynamique basée sur les positions - PBD 🎉.

Satisfaire les contraintes

Notre objectif lors de la boucle est de calculer le vecteur de correction qu’une particule doit se déplacer afin de satisfaire, ou de se rapprocher de la satisfaction, les contraintes.

Δx=ΔλM−1∇CxT\Delta \mathbf{x} = \Delta \lambda \mathbf{M}^{-1} \nabla C \mathbf{x}^T

où Δλ\Delta \lambda est défini comme suit :

Δλ=−C(x)∇C(x)M−1∇C(x)T+α~\Delta \lambda = \frac{-C(\mathbf{x})}{\nabla C(\mathbf{x}) \mathbf{M}^{-1} \nabla C(\mathbf{x})^T + \tilde{\alpha}}

Notez que α~=αΔt2\tilde{\alpha} = \frac{\alpha}{\Delta t^2} où α\alpha est la compliance de la contrainte. Rappelons que α=1k\alpha = \frac{1}{k} où kk est la raideur de la contrainte. C(x)C(\mathbf{x}) est l’équation de contrainte, ∇C(x)\nabla C(\mathbf{x}) est le gradient de ∇C(x)\nabla C(\mathbf{x}) et c’est donc un vecteur. M−1\mathbf{M}^{-1} est une matrice diagonale de masses inverses des particules participant à la contrainte.

Δλ\Delta \lambda, C(x)C(\mathbf{x}), et α~\tilde{\alpha} sont des valeurs scalaires.

En utilisant ces équations, nous allons simuler certaines contraintes avec du code ! 🖥️

La contrainte de distance

Pour commencer, nous parlerons de la contrainte de distance, car elle est plutôt facile à comprendre. L’objectif est de satisfaire la contrainte en déplaçant deux particules pour qu’elles se rapprochent à la longueur de repos, dd :

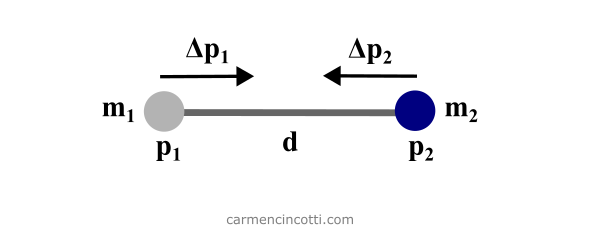
Distance constraint

où pp est la position d’une particule et mm est la masse.

Nous pouvons résoudre les équations de la section dernière afin de trouver les corrections de position finale, Δxn\Delta \mathbf{x}_n :

C(x1,x2)=∣x1,2∣−dn=x1,2∣x1,2∣Δx1C(x1,x2)=nΔx2C(x1,x2)=−n∴Δx1=−w1w1+w2(∣x1,2∣−d)n∴Δx2=+w2w1+w2(∣x1,2∣−d)n C(\mathbf{x_1}, \mathbf{x_2}) = |\mathbf{x}_{1,2}| - d\\[6pt] \mathbf{n} = \frac{\mathbf{x}_{1,2}}{|\mathbf{x}_{1,2}|}\\[6pt] \Delta_{\mathbf{x_1}}C(\mathbf{x_1}, \mathbf{x_2}) = \mathbf{n}\\[6pt] \Delta_{\mathbf{x_2}}C(\mathbf{x_1}, \mathbf{x_2}) = -\mathbf{n}\\[6pt] \therefore \Delta \mathbf{x_1} = - \frac{w_1}{w_1 + w_2}(|\mathbf{x}_{1,2}| - d) \mathbf{n}\\[6pt] \therefore \Delta \mathbf{x_2} = + \frac{w_2}{w_1 + w_2}(|\mathbf{x}_{1,2}| - d) \mathbf{n}\\[6pt]

La solution codée

Voici le code où je définis deux particules. La fonction distanceConstraint est basée sur le calcul de Δλ\Delta \lambda et la mise à jour immédiatement de la position, pp de la particule pnp_{n}. Il existe une contrainte de distance avec une longueur de repos égale à 11.

Vous remarquerez peut-être qu’il y a une petite astuce lors du calcul. Rappelons que le calcul pour trouver Δλ\Delta \lambda est :

Δλ=−C(x)∇C(x)M−1∇C(x)T+α~\Delta \lambda = \frac{-C(\mathbf{x})}{\nabla C(\mathbf{x}) \mathbf{M}^{-1} \nabla C(\mathbf{x})^T + \tilde{\alpha}}

Heureusement, ∇C(x)\nabla C(\mathbf{x}) est un vecteur normalisé. Alors :

∇C(x)T∇C(x)=1\nabla C(\mathbf{x})^T\nabla C(\mathbf{x}) = 1

Nous pouvons donc simplifier notre équation comme suit :

Δλ=−C(x)M−1+α~\Delta \lambda = \frac{-C(\mathbf{x})}{\mathbf{M}^{-1} + \tilde{\alpha}}

Enfin, j’ai utilisé une fonction de logging pour voir comment les particules se bougent avant et après la boucle de simulation :

BEFORE APPLYING XPBD LOOP ------------------------- POSITION P1: [ '2.0000', '2.0000', '0.0000' ] POSITION P2: [ '-2.0000', '-2.0000', '0.0000' ] AFTER APPLYING XPBD LOOP ------------------------ POSITION P1: [ '0.3536', '0.3536', '0.0000' ] POSITION P2: [ '-0.3536', '-0.3536', '0.0000' ]

Nous voyons que les deux particules se rapprochent et se déplacent jusqu’aux points p1=(.3536,.3536,0),p2=(−.3536,−.3536,0)p_1 = (.3536, .3536, 0), p_2 = (-.3536, -.3536, 0). Est-ce que ces nouveaux points satisfont la contrainte de distance ? Rappelons que la longueur de repos est égale à 11 :

.35362+.35362+.35362+.35362≈1\sqrt{.3536^2 + .3536^2} + \sqrt{.3536^2 + .3536^2} \\[6pt] \approx 1

Oui ! La contrainte de distance a été satisfaite !

Prochainement…

On verra ensemble la contrainte de flexion isométrique. Restez à l’écoute !

Des ressources (en français et anglais)

Comments for La contrainte de distance | XPBD

Written by Carmen Cincotti, computer graphics enthusiast, language learner, and improv actor currently living in San Francisco, CA.  Follow @CarmenCincotti

Contribute

Interested in contributing to Carmen's Graphics Blog? Click here for details!