Carmen's Graphics Blog

Computer Graphics and Physics Simulation Tutorials and Articles
PostsAboutProjectsJobs

La contrainte de flexion isométrique | XPBD

XPBD utilise des contraintes de particules pour s'assurer que les particules se déplacent d'une certaine manière, par rapport aux autres particules. Examinons de plus près une contrainte commune que nous trouverons dans une simulation de tissu, la contrainte de flexion isométrique.

Keywords: dynamique basée sur la position, simulation de tissu, lagrange, physique, infographie, tutoriel

By Carmen Cincotti  

Une grande pièce du puzzle de XPBD, dont nous avons déjà parlé il y a quelques semaines, est la satisfaction des contraintes de particules. Les contraintes de particules forcent une particule à se déplacer et à agir d’une certaine manière, par rapport aux autres particules dans le système.

How a particle moves back to the string

Si vous me suiviez depuis quelques mois, vous connaissez sans doute mon objectif de simuler le tissu 🧵. La semaine dernière, nous avons parlé de la contrainte de distance. Cette semaine, nous nous concentrerons sur les contraintes de flexion isométrique.

Encore une fois, je vous présente ces fameux articles que nous avons déjà étudiés lors d’un article il y a quelques semaines sur XPBD que je vais référencer pour les maths au cours de ce post :

Un résumé de XPBD

Rappelons que l’algorithme de XPBD à petits pas est défini comme suit :

Algorithm of XPBD with small steps

⚠️ Comme je l’ai dit, nous avons déjà parlé de cet algorithme à fond et je vous recommande de lire l’article si vous êtes déjà perdu.

Pour l’instant, seule la boucle qui se trouve dans les lignes (6) - (11) nous intéresse. Comme vous pouvez le voir, la fonction de cette boucle est de satisfaire les contraintes de la simulation afin de corriger directement les positions de chaque particule qui participe aux contraintes.

On vient de couvrir la raison pour laquelle cette méthode de simulation s’appelle la dynamique basée sur les positions - PBD 🎉.

Satisfaire les contraintes

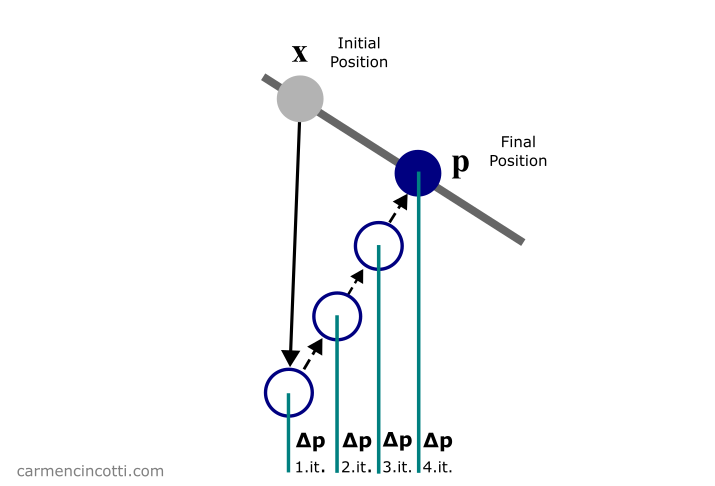
Notre objectif lors de la boucle est de calculer le vecteur de correction qu’une particule doit se déplacer afin de satisfaire, ou de se rapprocher de la satisfaction, les contraintes.

Δx=ΔλM−1∇CxT\Delta \mathbf{x} = \Delta \lambda \mathbf{M}^{-1} \nabla C \mathbf{x}^T

où Δλ\Delta \lambda est défini comme suit :

Δλ=−C(x)∇C(x)M−1∇C(x)T+α~\Delta \lambda = \frac{-C(\mathbf{x})}{\nabla C(\mathbf{x}) \mathbf{M}^{-1} \nabla C(\mathbf{x})^T + \tilde{\alpha}}

Notez que α~=αΔt2\tilde{\alpha} = \frac{\alpha}{\Delta t^2} où α\alpha est la compliance de la contrainte. Rappelons que α=1k\alpha = \frac{1}{k} où kk est la raideur de la contrainte. C(x)C(\mathbf{x}) est l’équation de contrainte, ∇C(x)\nabla C(\mathbf{x}) est le gradient de ∇C(x)\nabla C(\mathbf{x}) et c’est donc un vecteur. M−1\mathbf{M}^{-1} est une matrice diagonale de masses inverses des particules participant à la contrainte.

Δλ\Delta \lambda, C(x)C(\mathbf{x}), et α~\tilde{\alpha} sont des valeurs scalaires.

En utilisant ces équations, nous allons simuler certaines contraintes avec du code ! 🖥️

La contrainte de flexion isométrique

Parlons maintenant de la contrainte de flexion isométrique. Voici un exemple de ce à quoi cela pourrait ressembler lors d’une simulation de tissu :

Bending cloth example

La contrainte de flexion isométrique est une contrainte de flexion pour les surfaces inextensibles. Fondamentalement, c’est un excellent modèle de flexion pour les simulations de tissu en raison du fait que le tissu ne peut normalement pas être étiré (bien que cela dépende du matériau).

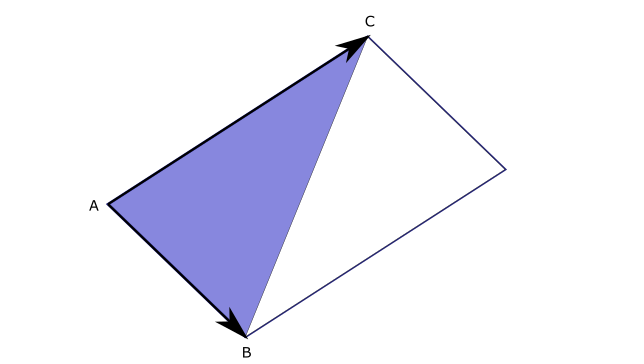
La contrainte se compose de quatre particules qui forment une configuration de deux triangles, qui ressemble à ce qui suit :

Four triangles configuration

où chaque cercle violet est une particule à un emplacement xn\mathbf{x}_n. Les arêtes des deux triangles sont étiquetées comme ene_n. Cette configuration s’appelle un stencil.

Pour calculer le déplacement nécessaire d’une particule afin de satisfaire la contrainte - on commence d’abord par l’équation de la contrainte de flexion isométrique :

Cbend(xs)=12∑i,jQi,jxiTxj C_{bend}(\mathbf{x}_s) = \frac{1}{2}\sum_{i,j}\mathbf{Q}_{i,j}\mathbf{x}_{i}^T\mathbf{x}_{j}

Quoi 😨 ?! Ne t’inquiétez pas, nous allons décomposer petit à petit cette équation.

On commence avec la matrice Qi,j∈R4x4\mathbf{Q}_{i,j} \in \mathbb{R}^{\text{4x4}}, qui est l’énergie de flexion hessienne constante locale. Cette ressource donne la dérivation.

Nous initialisons une seule fois la matrice Q\mathbf{Q} pour chaque configuration de quatre particules. Rappelons que la matrice hessienne comprend les dérivées partielles du second ordre :

Qi,j(f)=∂2f∂xi∂xj \mathbf{Q}_{i,j}(f) = \frac{\partial^2 f}{\partial{x}_i\partial{x}_j}

Afin de trouver Qi,j\mathbf{Q}_{i,j}, on utilise l’équation :

Q=3A0+A1KTK \mathbf{Q} = \frac{3}{A_0 + A_1}\mathbf{K}^T\mathbf{K}

où A0A_0 et A1A_1 sont des aires des triangles adjacents. Rappelons que nous pouvons trouver l’aire d’un triangle si les emplacements de ses trois points sont donnés avec une petite astuce d’algèbre linéaire :

Finding area of triangle with cross product

A=12∣AB⃗×AC⃗∣A = \frac{1}{2}|\vec{AB} \times \vec{AC}|

K\mathbf{K} est un vecteur qui se compose des cotangentes entres les arêtes du triangle cjk=cot⁡∠ej,ekc_{jk} = \cot\angle e_j,e_k :

K=[c01+c04,c02+c03,−c01−c02,−c03−c04] \mathbf{K} = [c_{01} + c_{04}, c_{02} + c_{03}, -c_{01} - c_{02}, -c_{03} - c_{04}]

Comment trouver la cotangente entre deux vecteurs 🤔

La cotangente est définie comme suit :

cot⁡θ=cos⁡θsin⁡θ \cot \theta = \frac{\cos \theta}{\sin \theta}

Nous pouvons trouver cos⁡θ\cos \theta avec le produit scalaire :

a⋅b=∣a∣×∣b∣×cos⁡θ∴cos⁡θ=a⋅b∣a∣×∣b∣ \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| \times |\mathbf{b}| \times \cos \theta \\[6pt] \therefore \cos \theta = \frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a}| \times |\mathbf{b}|}

Pour trouver sin⁡θ\sin \theta, on utilise le produit croisé :

∣a×b∣=∣a∣∣b∣sin⁡θ∴sin⁡θ=∣a×b∣∣a∣×∣b∣ |\mathbf{a} \times \mathbf{b}| = |\mathbf{a}| |\mathbf{b}| \sin \theta \\[6pt] \therefore \sin \theta = \frac{|\mathbf{a} \times \mathbf{b}|}{|\mathbf{a}| \times |\mathbf{b}|}

On peut donc réécrire l’équation de cot⁡θ\cot \theta comme suit :

cot⁡θ=cos⁡θsin⁡θ=a⋅b∣a∣×∣b∣∣a×b∣∣a∣×∣b∣=a⋅b∣a×b∣ \cot \theta = \frac{\cos \theta}{\sin \theta} \\[6pt] = \frac{\frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a}| \times |\mathbf{b}|}}{\frac{|\mathbf{a} \times \mathbf{b}|}{|\mathbf{a}| \times |\mathbf{b}|}} \\[6pt] = \frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a} \times \mathbf{b}|}

Revenons maintenant à cette équation :

Cbend(xs)=12∑i,jQi,jxiTxj C_{bend}(\mathbf{x}_s) = \frac{1}{2}\sum_{i,j}\mathbf{Q}_{i,j}\mathbf{x}_{i}^T\mathbf{x}_{j}

x\mathbf{x} est les emplacements des particules. Enfin, nous avons besoin du gradient ∇Cbend\nabla C_{bend} pour trouver Δλ\Delta \lambda qui est défini comme suit :

∇Cbend=∑jQi,jxj \nabla C_{bend} = \sum_{j}\mathbf{Q}_{i,j}\mathbf{x}_{j}

Nous avons désormais toutes les équations dont nous avons besoin. Je trouve que ces équations sont difficiles à vraiment comprendre sans les voir fonctionner dans le code. Alors, regardons un peu de code maintenant !

Le code

Si vous avez déjà vu le code de la contrainte de distance de l’article dernier, vous noterez que la boucle de simulation ne change pas. On se concerne uniquement par la fonction bendingConstraint.

Heureusement, le code n’est pas sorcier. Nous devons d’abord calculer C, puis le gradient - grad, qui est ∇C\nabla C. Ensuite, nous trouvons deltaLagrangianMultiplier qui est Δλ\Delta \lambda. Enfin, on trouve Δx\Delta \mathbf{x}, qui est le déplacement d’une particule pendant un sous-pas (substep) dans le temps.

Lors de l’exécution du programme - nous devrions voir les éléments suivants enregistrés sur la console :

BEFORE APPLYING XPBD LOOP ------------------------- POSITION P1: [ '0.0000', '0.0000', '0.0000' ] POSITION P2: [ '0.0000', '1.0000', '0.0000' ] POSITION P3: [ '-0.5000', '0.5000', '0.0000' ] POSITION P4: [ '0.5000', '0.5000', '0.0000' ] VELOCITY P1: [ '0.0000', '0.0000', '0.0000' ] VELOCITY P2: [ '0.0000', '0.0000', '0.0000' ] VELOCITY P3: [ '0.0000', '0.0000', '0.0000' ] VELOCITY P4: [ '0.0000', '0.0000', '0.0000' ] AFTER APPLYING XPBD LOOP ------------------------ POSITION P1: [ '0.0000', '0.0000', '0.0000' ] POSITION P2: [ '0.0000', '1.0000', '0.0000' ] POSITION P3: [ '-0.5000', '0.5000', '0.0000' ] POSITION P4: [ '0.5000', '0.5000', '0.0000' ] VELOCITY P1: [ '0.0000', '0.0000', '0.0000' ] VELOCITY P2: [ '0.0000', '0.0000', '0.0000' ] VELOCITY P3: [ '0.0000', '0.0000', '0.0000' ] VELOCITY P4: [ '0.0000', '0.0000', '0.0000' ]

Génial ! Il ne reste plus qu’à intégrer ces contraintes dans la simulation du tissu ! À la prochaine !

Des ressources (en français et anglais)

Comments for La contrainte de flexion isométrique | XPBD

Written by Carmen Cincotti, computer graphics enthusiast, language learner, and improv actor currently living in San Francisco, CA.  Follow @CarmenCincotti

Contribute

Interested in contributing to Carmen's Graphics Blog? Click here for details!