La contrainte de flexion la plus performante | XPBD

XPBD utilise des contraintes de particules pour s'assurer que les particules se déplacent d'une certaine manière, par rapport aux autres particules. Jetons un coup d'œil à une contrainte de flexion qui sera super performante pour créer des visualisations fluides et visuellement agréables.

Keywords: dynamique basée sur la position, simulation de tissu, lagrange, physique, infographie,

By Carmen Cincotti

September 05, 2022Updated September 12, 2022

Un résumé de XPBD
Satisfaire les contraintes
La contrainte de flexion la plus performante
Le code
- Comment trouver des triangles adjacents
- Le code de la contrainte de flexion performant
Des ressources (en français et anglais)

Une grande pièce du puzzle de XPBD, dont nous avons déjà parlé il y a quelques semaines, est la satisfaction des contraintes de particules. Les contraintes de particules forcent une particule à se déplacer et à agir d’une certaine manière, par rapport aux autres particules dans le système.

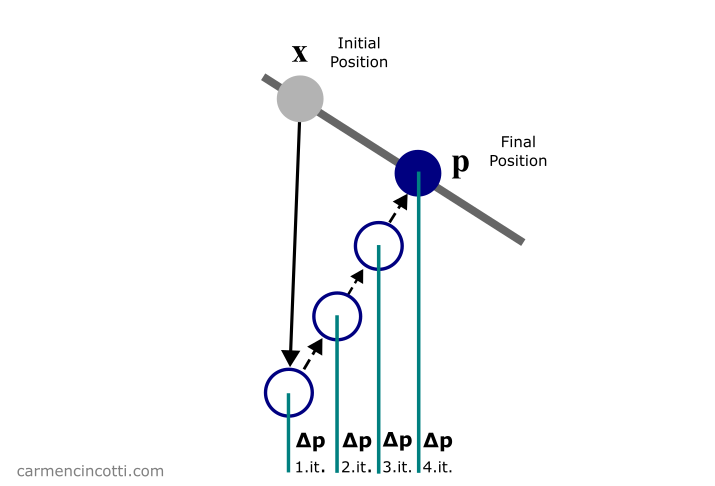
How a particle moves back to the string

Si vous me suiviez depuis quelques mois, vous connaissez sans doute mon objectif de simuler le tissu 🧵. Ces semaines dernières, nous avons parlé de la contrainte de distance et de la contrainte de flexion isométrique. Cette semaine, nous nous concentrerons sur une contrainte de flexion plus performante.

Pourquoi changer de cap ? Car la contrainte de flexion isométrique est trop chère à résoudre 🥵. Matthias Müller nous montre une alternative pour simuler la flexion avec d’excellents résultats !

Encore une fois, je vous présente ces fameux articles que nous avons déjà étudiés lors d’un article il y a quelques semaines sur XPBD que je vais référencer pour les maths au cours de ce post :

Un résumé de XPBD

Rappelons que l’algorithme de XPBD à petits pas est défini comme suit :

Algorithm of XPBD with small steps

⚠️ Comme je l’ai dit, nous avons déjà parlé de cet algorithme à fond et je vous recommande de lire l’article si vous êtes déjà perdu.

Pour l’instant, seule la boucle qui se trouve dans les lignes (6) - (11) nous intéresse. Comme vous pouvez le voir, la fonction de cette boucle est de satisfaire les contraintes de la simulation afin de corriger directement les positions de chaque particule qui participe aux contraintes.

On vient de couvrir la raison pour laquelle cette méthode de simulation s’appelle la dynamique basée sur les positions - PBD 🎉.

Satisfaire les contraintes

Notre objectif lors de la boucle est de calculer le vecteur de correction qu’une particule doit se déplacer afin de satisfaire, ou de se rapprocher de la satisfaction, les contraintes.

\Delta \mathbf{x} = \Delta \lambda \mathbf{M}^{-1} \nabla C \mathbf{x}^T

où $\Delta \lambda$ est défini comme suit :

\Delta \lambda = \frac{-C(\mathbf{x})}{\nabla C(\mathbf{x}) \mathbf{M}^{-1} \nabla C(\mathbf{x})^T + \tilde{\alpha}}

Notez que $\tilde{\alpha} = \frac{\alpha}{\Delta t^2}$ où $\alpha$ est la compliance de la contrainte. Rappelons que $\alpha = \frac{1}{k}$ où $k$ est la raideur de la contrainte. $C(\mathbf{x})$ est l’équation de contrainte, $\nabla C(\mathbf{x})$ est le gradient de $\nabla C(\mathbf{x})$ et c’est donc un vecteur. $\mathbf{M}^{-1}$ est une matrice diagonale de masses inverses des particules participant à la contrainte.

$\Delta \lambda$ , $C(\mathbf{x})$ , et $\tilde{\alpha}$ sont des valeurs scalaires.

En utilisant ces équations, nous allons simuler certaines contraintes avec du code ! 🖥️

La contrainte de flexion la plus performante

Dans cette présentation de Matthias Müller, Matthias nous montre une alternative pour intégrer une contrainte de flexion sans faire de calculs complexes et chers. Heureusement, elle ressemble beaucoup à la contrainte de distance dont nous avons déjà parlé il y a quelques semaines dans cet article.

Voici une image qui montre exactement ce que nous essayons d’accomplir :

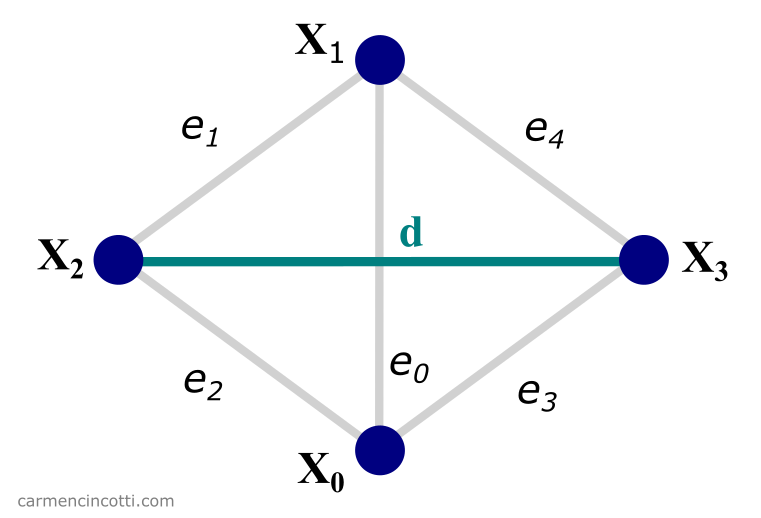
More performant bending constraint

Comme vous pouvez le voir, il n’y a qu’une seule contrainte de distance entre deux particules de deux triangles adjacents. Bien sûr, cette méthode est un peu plus complexe qu’une contrainte de distance, car il faut d’abord trouver des triangles qui sont adjacents les uns aux autres.

Ensuite, nous suivons le même processus que nous suivions pour satisfaire la contrainte de distance. 😮‍💨

Nous pouvons résoudre les équations de la section dernière afin de trouver les corrections de la position finale, $\Delta \mathbf{x}_n$ :

C(\mathbf{x_2}, \mathbf{x_3}) = |\mathbf{x}_{2,3}| - d\\[6pt] \mathbf{n} = \frac{\mathbf{x}_{2,3}}{|\mathbf{x}_{2,3}|}\\[6pt] \Delta_{\mathbf{x_2}}C(\mathbf{x_2}, \mathbf{x_3}) = \mathbf{n}\\[6pt] \Delta_{\mathbf{x_3}}C(\mathbf{x_2}, \mathbf{x_3}) = -\mathbf{n}\\[6pt] \therefore \Delta \mathbf{x_2} = - \frac{w_2}{w_2 + w_3}(|\mathbf{x}_{2,3}| - d) \mathbf{n}\\[6pt] \therefore \Delta \mathbf{x_3} = + \frac{w_3}{w_2 + w_3}(|\mathbf{x}_{2,3}| - d) \mathbf{n}\\[6pt]

Le code

Heureusement, nous allons voir que le code de cette contrainte est presque similaire à la contrainte de distance. Avant de le voir, il faut d’abord comprendre comment trouver deux triangles adjacents.

Comment trouver des triangles adjacents

Imaginons que nous chargeons un maillage avec qui se compose de 1.000 triangles. Comment pourrions-nous déterminer quels triangles sont adjacents les uns aux autres ? Heureusement, il existe une petite astuce :

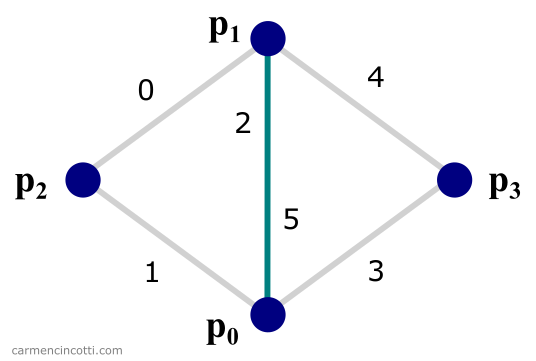
Adjacent edges

Comme vous pouvez le voir, il y a deux triangles qui partagent une arête (2 et 5). Nous pouvons exploiter ce faite ! Nos étapes sont les suivantes :

Créer un tableau dans lequel nous pouvons rechercher des arêtes partagées entre deux triangles.
Utiliser ce tableau afin de trouver les quatre points qui forment deux triangles, comme sur l’image ci-dessus.

On crée d’abord une liste composée des arêtes avec des ids globaux qui se trouvent entre chaque paire de particules. C’est notre travail d’étiqueter chaque arête.

Par exemple, imaginons que nous créons une liste d’arêtes de cette image :

Adjacent edges

p_id₀	p_id₁	e_i
0	1	2
1	2	0
2	0	1
0	3	3
3	1	4
1	0	5

Vous pouvez sans doute voir que les particules $p_0$ et $p_1$ partagent les arêtes globales (2) et (5). Pour trouver cette paire dans le code, nous trions le tableau d’arêtes dans l’ordre croissant par le numéro d’identification, id, de chaque particule dans chaque paire :

p_id₀	p_id₁	e_i
0	1	2
0	1	5
0	2	1
0	3	3
1	2	0
1	3	4

Ensuite, on crée un tableau de voisins, ou neighbors en anglais, qui est initialisé avec -1s, où -1 qui signifie ‘pas de voisin’. Si nous créons correctement un tableau de voisins, nous verrions un tableau de voisins comme suit :

[n_{e0}, n_{e1}, n_{e2}, n_{e3}, n_{e4}] \rightarrow [-1, -1, 5, -1, -1, 2]

Voici le code d’une fonction, findTriNeighbors, qui nous aidera à créer cette liste de voisins, ou neighbors :

Si vous avez suivi mes posts jusqu’à présent, vous saurez bien que je n’utilise que WebGPU et JavaScript, sans une librairie comme ThreeJS. Je dis cela parce que vous aurez besoin d’accéder au tampon d’index dont nous avons déjà parlé dans cet article.

Cette liste de voisins sera essentielle pour la prochaine étape.

Avec notre tableau de voisins, ou neighbors, on doit créer une liste contenant l’identifiant de chaque particule dans le quatuor qui forme chaque paire de triangles. Elle sera utilisée afin de placer une contrainte de distance entre les particules opposées comme sur l’image ci-dessous :

More performant bending constraint

Le processus de le faire est illustré sur l’image ci-dessous :

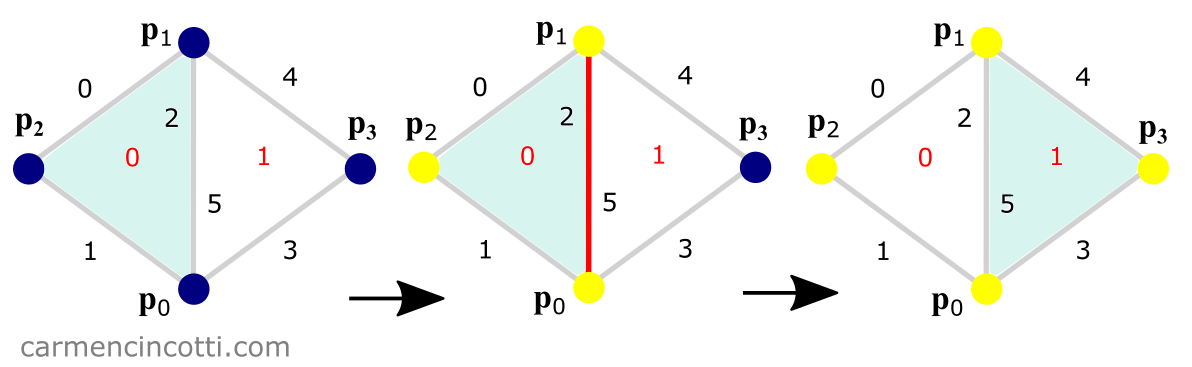
Method to find tri pair ids

On visite chaque face de notre maillage pour déterminer s’il y a une arête partagée (en recherchant dans la liste des arêtes voisines, neighbors, que nous venons de remplir dans l’étape dernière). Si oui, nous enregistrons les trois sommets de ce triangle et après on visite le triangle adjacent - où nous enregistrons le quatrième sommet de la configuration.

Voici la fonction getTriPairIds qui fait exactement cela :

Avec notre liste de triPairIds, on est prêt à avancer à la satisfaction de la contrainte ! 🎉

Le code de la contrainte de flexion performant

Comme vous pouvez le voir, le code est presque le même du code de la contrainte de distance. Utilisez simplement les deux sommets qui ne sont pas partagés au lieu de deux sommets adjacents lors du calcul des corrections de position finale !

Carmen's Graphics Blog