Une table de hachage spatiale est un type particulier de table de hachage, qui est un sujet dont nous avons déjà beaucoup parlé en détail.
Les tables de hachage spatiales traitent des positions dans l’espace.
Une table de hachage spatiale est un bon outil pour détecter les collisions entre objets et particules, ce qui s’avérera utile pour des simulations de tissu, des moteurs physiques de jeux vidéo, etc.
Voyons ensemble comment fonctionne une telle structure !
Une revue des tables de hachage
Avant de continuer, je vous suggère que si vous n’avez pas déjà lu les articles précédents sur l’adressage ouvert et les tables de hachage, je vous recommande vraiment d’y jeter un coup d’œil afin de pouvoir suivre plus facilement :
Qu’est-ce qu’une table de hachage spatiale ?
Une table de hachage spatiale ressemble à une table de hachage ordinaire. Cependant, la différence la plus frappante est qu’une table de hachage spatiale utilise des emplacements (2D ou 3D) dans l’espace comme clés de hachage pour entrer dans la table.
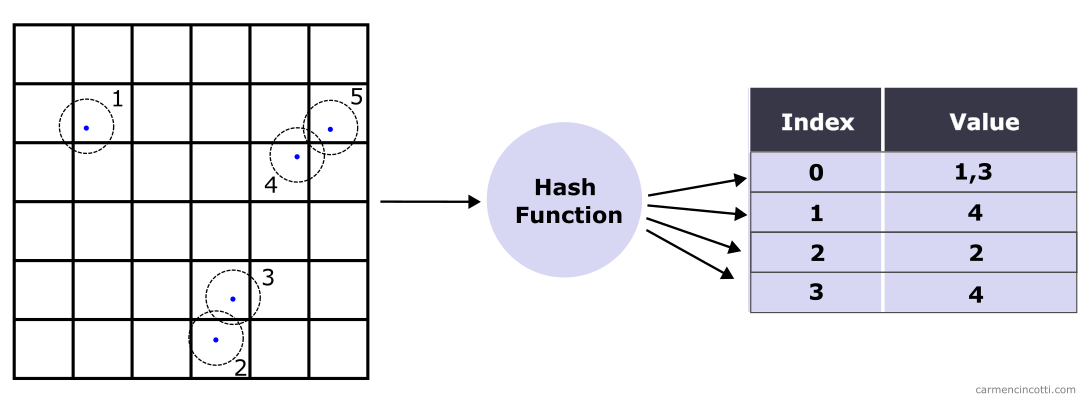
Voyons ensemble un exemple.
Un exemple
Pour cet exemple, il y a une particule qui s’est installée dans l’espace à la position .

Pour stocker cette particule dans une table de hachage, on utilise une fonction de hachage qui prend comme entrée la position de la particule.

La fonction de hachage nous renvoie un entier qui sert d’indice dans la table de hachage spatiale. La particule est stockée à cet indice.

Comment hacher une position
J’utilise cette fonction qui vient de Matthias Müller :
hashCoords(xi: number, yi: number, zi: number) {
const hash = (xi * 92837111) ^ (yi * 689287499) ^ (zi * 283923481);
return Math.abs(hash);
}
L’idée est de renvoyer un entier pseudoaléatoire. Ainsi, la fonction de hachage est moins susceptible de renvoyer des hachages qui causent des collisions de hachage.
Table de hachage spatiale dense
Une implémentation dense d’une table de hachage spatiale a été proposée par l’auteur de Ten Minute Physics, Matthias Müller lors d’une de ses vidéos.
L’implémentation dense nous offre une complexité temporelle et spatiale très efficiente.
Seuls deux tableaux sont utilisés. :
- Tableau de particule - Il stocke les références aux particules elles-mêmes.
- Tableau de comptage - Il stocke le nombre de particules hachées dans un seau particulier, qui sert finalement de l’indice dans le Tableau de particule.

On verra comment ceci fonctionne dans la partie suivante !
Comment remplir une table de hachage dense
Pour clarifier cette idée, voyons d’étape en étape comment remplir une table de hachage dense.
Espace délimité
On commence avec cinq particules dans l’espace comme ceci :
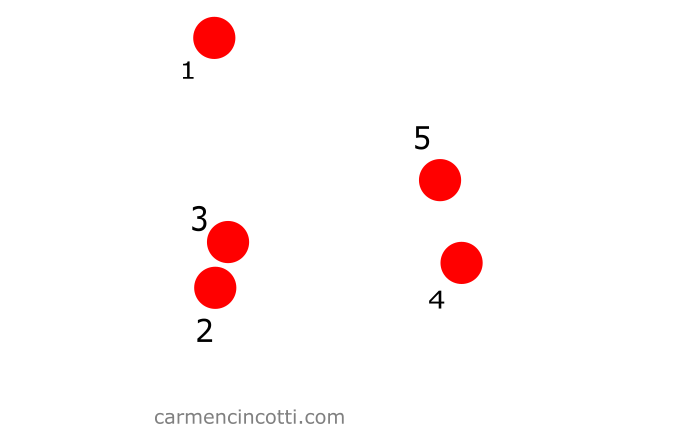
Étape 1 : Créer une grille
Imaginons que nous créons une grille superposée sur nos particules :
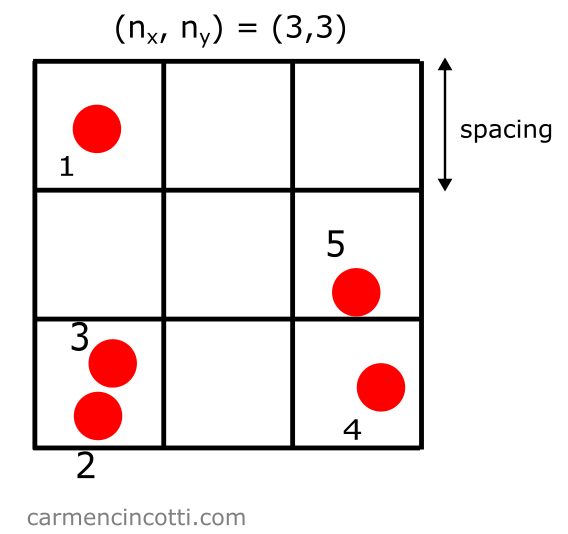
Définissons quelques propriétés de cette grille
- Espacement (spacing) : la taille de chaque carré de la grille. Une bonne règle empirique consiste à définir l’espacement comme deux fois le rayon d’une particule, .
- : le nombre de carrés dans chaque direction (et dans le cas 3D).
À ce stade, c’est notre travail de créer un tableau qui représente une telle grille. Parce que ce tableau va être désigné pour compter des particules dans chaque carré de la grille - nous l’appellerons cellCount :

Ajouter un espace supplémentaire
Note : On ajoute un espace supplémentaire qui sera utile lorsqu’on fait une requête - ou un query - pour les particules qui se trouvent autour d’un emplacement d’intérêt. Ignorez cela pour le moment, nous y reviendrons plus tard !
Étape 2 : Remplir le tableau de comptage
Ensuite, nous parcourons toutes les particules pour remplir cellCount. Pour chaque particule qui appartient à un seau particulier, on incrémente le compteur de .

Comment calculer le seau auquel appartient une particule
Nous utilisons la position d’une particule. Voici une méthode potentielle pour calculer l’indice que nous allons utiliser pour indexer dans cellCount :
… et en 3D :
Avoir une particule à la position et une table avec une taille de et avec spacing égal à nous donne :
L’indice est égal à .
Comme vous l’avez probablement déjà compris, cet exemple que nous venons de voir dépend de plusieurs variables, comme l’emplacement de l’origine. Utilisez cet exemple comme guide et non comme solution.
Étape 3 : Calculer la somme partielle
La prochaine étape est facile. Nous devons calculer la somme partielle sur le tableau cellCount. Nous pouvons l’écraser avec ces nouvelles valeurs.

Étape 4 : Remplir le tableau de particules
Enfin, nous parcourons sur toutes les particules pour les stocker dans le tableau particleMap (la table de particules).

Prenons par exemple la particule :
- Tout d’abord, on index dans
cellCountà l’indice , car la particule est là. - Ensuite, on décrément
cellCountà cet indice, ce qui change l’entier stocké ici de à . - Ce nouvel entier est utilisé comme indice dans
particleMap. Nous stockons la particule à l’indice dansparticleMap.
Vous pouvez bien sûr rendre cette méthode plus performant en combinant quelques étapes afin d’éviter plusieurs boucles supplémentaires.
Espace illimité
Commençons avec cinq particules dans un espace illimité comme ceci :

Note bien que dans cet exemple, l’espace est illimité. Le processus de la section précédente n’est donc plus suffisant !
Étape 1 : Créer une grille
Dans ce cas, la grille est illimitée :
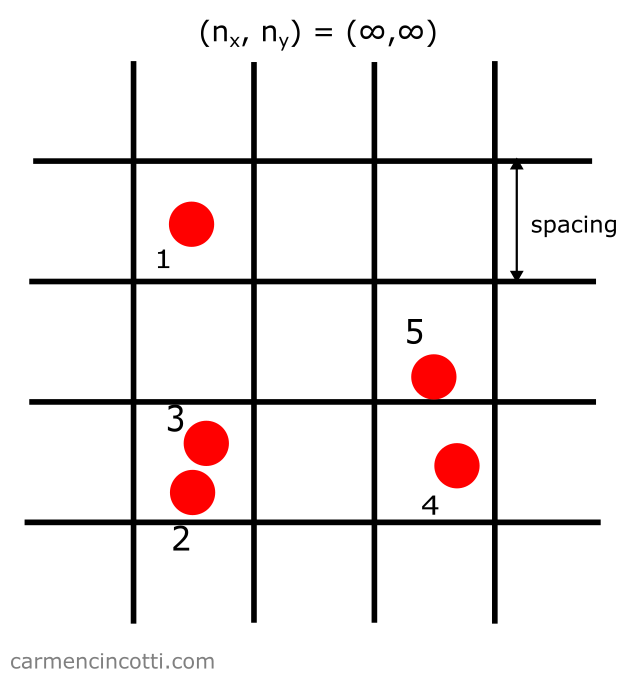
Ce n’est donc pas une bonne idée d’essayer de représenter une telle structure avec un tableau sous-jacent de stockage d’une taille égale, car on risque de trop gaspiller trop de mémoire.
Comment éviter ce problème ?
La réponse : On crée un tableau de taille fixe auquel ajouter toutes les particules. Cette implémentation nécessitera de résoudre les collisions de hachage !
Il faut définir deux paramètres :
- Espacement (spacing) : la taille de chaque carré de la grille. Une bonne règle empirique consiste à définir l’espacement comme deux fois le rayon d’une particule, .
- La taille de la table : La taille (
tableSize) du tableau sous-jacent de stockage (cellCount).
Dans ce cas - on définit tableSize égale à 9 plus 1, ce qui fait 10 :
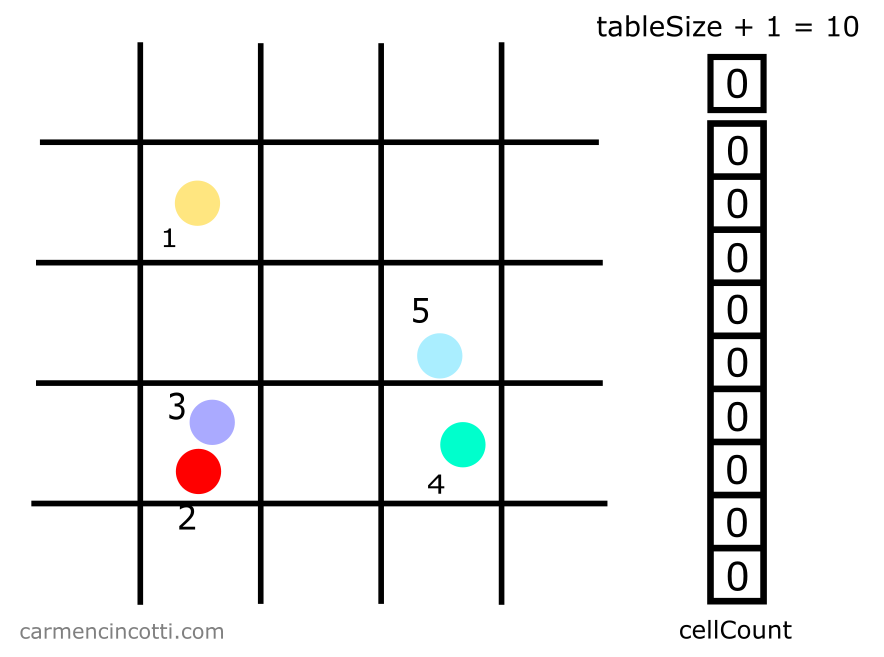
Étape 2 : Remplir le tableau de comptage
Ensuite, nous parcourons toutes les particules pour remplir cellCount. Cette fois, nous utilisons une fonction de hachage pour indexer dans cellCount afin d’insérer des particules.

Pour indexer dans le tableau, nous pouvons utiliser cette formule :
Mais qu’est-ce que et ? Nous pourrions naïvement les définir comme les coordonnées de la particule elle-même, mais cela signifierait que les particules d’un même carré pourraient potentiellement être hachées dans différents seaux !
Par conséquent nous devons normaliser les coordonnées d’une particule à la place de la position du carré dans lequel elle réside.
Pour le faire, nous pouvons utiliser la fonction hashPos qui appelle intCoord, qui renvoie une coordonnée d’un carré dans la grille :
intCoord(coord: number) {
return Math.floor(coord / spacing);
}
hashPos() {
return hashCoords(
intCoord(pos_x),
intCoord(pos_y),
intCoord(pos_z)
);
}
Et nous avons déjà défini notre fonction de hachage, hashCoords, ci-dessus.
Nous pouvons maintenant garantir que toutes les particules dans un certain carré de la grille seront hachées au même endroit.
Comment résoudre les collisions de hachage
Comme vous pouvez le voir, les particules et se résolvent au même seau. Il nous suffit d’incrémenter l’entier dans cellCount à cet indice. Nous verrons pourquoi cela fonctionne dans les étapes suivantes.
Étape 3 : Calculer la somme partielle
Comme avant, nous devons calculer la somme partielle sur le tableau cellCount. Nous pouvons l’écraser avec ces nouvelles valeurs.

Étape 4 : Remplir le tableau de particules
Enfin, nous parcourons toutes les particules pour les stocker dans le tableau particleMap (la table de particules).
Prenons par exemple la particule :
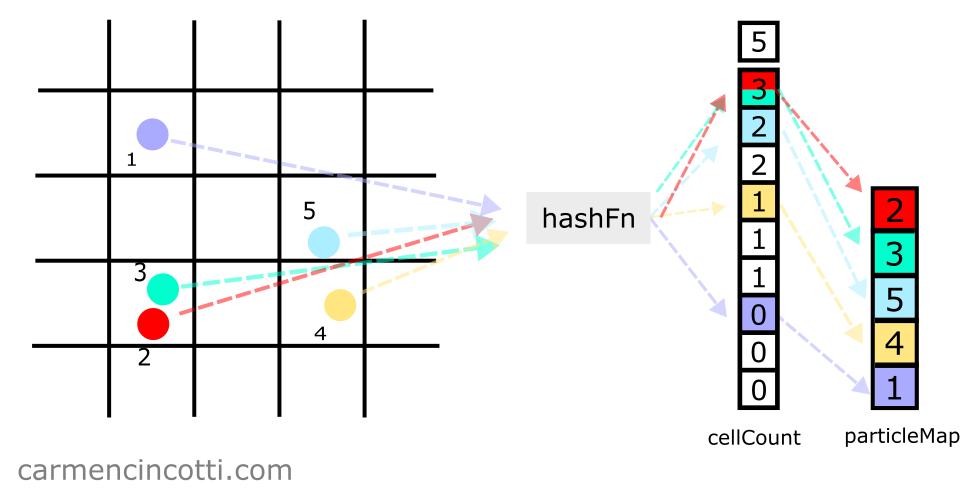
- Tout d’abord, on index dans
cellCountà l’indice , car la particule est hachée vers cet emplacement. - Ensuite, on décrément
cellCountà cet indice, ce qui change l’entier stocké ici de à . - Ce nouvel entier est utilisé comme indice dans
particleMap. Nous stockons donc la particule à l’indice dansparticleMap.
Prochainement…
On verra comment effectuer des requêtes dans la table de hachage spatiale, et voir le code d’une telle structure !
