Je voudrais poursuivre notre conversation sur les tables de hachage spatiales dont nous avons commencé à apprendre la semaine dernière.
Les tables de hachage spatiales nous permettront d’implémenter une fonctionnalité très importante des simulations de tissus : les autocollisions.
Qu’est-ce qu’une autocollision de tissu ?
Une autocollision est l’interaction qui se produit lorsque les particules d’un morceau de tissu entrent en collision les unes contre les autres.

Comment interroger une table de hachage spatiale :
Voyons ensemble comment interroger une table de hachage spatiale afin de détecter des particules proches les unes des autres, tout en gardant une complexité temporelle rapide.
Étape 1 : Créer la table de hachage spatiale et la remplir
Nous avons déjà fait cela lors de l’article précédent. Je vous conseille de le lire avant de continuer !
Avec nos deux tableaux, cellCount et particleMap, nous sommes prêts à rechercher des particules à proximité.
Étape 2 : Interroger des carrés adjacents
Notre but dans cette étape est de trouver toutes les particules qui se trouvent dans des carrés adjacents afin de limiter la recherche aux particules proches. Cette méthode est très rapide par rapport à une méthode qui vérifie chaque particule pour voir si elles sont proches ou non.
Pour effectuer une telle requête, on définit une distance de recherche maximale, maxDist. Imaginons que j’ai déjà défini maxDist égal à la longueur d’un carré que je voudrais rechercher des particules proches de la particule :

Comme vous pouvez le voir, j’ai marqué en violet tous les points que nous finirons par interroger.
Maintenant, nous allons parcourir tous ces points violets afin de voir si les carrés dans lesquels ils résident contiennent des particules. Nous devrons également vérifier le carré dans lequel se trouve la particule .
Pour l’instant, voyons un exemple sur la façon de vérifier les particules dans un carré d’intérêt.
Je vais interroger le point violet en haut à gauche. On commence par calculant la coordonnée de la grille, squareCoordinate, dans laquelle ce point se trouve. Pour le faire, on utilise la fonction intCoord :
intCoord(pos: number) {
return Math.floor(pos / spacing);
}
const squareCoordinates = [
intCoord(pos.x),
intCoord(pos.y),
]
En utilisant squareCoordinate, nous pouvons indexer dans cellCount pour voir quelles particules s’y trouvent…
Rappelons que nous pouvons utiliser la fonction de hachage hashPos pour calculer le hachage d’une position :
hashCoords(xi: number, yi: number, zi: number) {
const hash = (xi * 92837111) ^ (yi * 689287499) ^ (zi * 283923481);
return Math.abs(hash);
}
hashPos(squareCoordinates) {
return hashCoords(
...squareCoordinates
);
}
Supposons que nous utilisons une fonction de hachage qui, en hachant squareCoordinates, l’indice nous est renvoyé :

Pour voir s’il y a des particules dans cet espace, on effectue le calcul suivant :
où est l’indice qu’on vient de calculer.
En poursuivant cet exemple, nous constatons qu’il n’y a rien dans la table à l’index ! :
Voyons maintenant un exemple d’un carré dans lequel résident des particules. Interrogeons la coordonnée située en bas :

En hachant squareCoordinate, nous obtenons l’indice . Avec cet indice, nous interrogeons le tableau cellCount pour les particules comme avant :
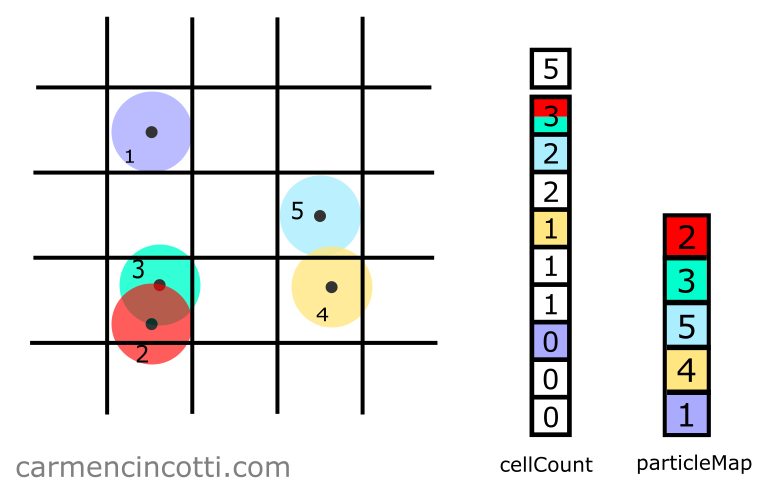
Cette fois, nous voyons qu’une particule existe dans le carré d’intérêt ! Le nombre à cellCount[i] sert également à indexer dans particleMap, qui dans ce cas est .
Par conséquent, en indexant dans particleMap avec l’index , nous pouvons voir que la particule se trouve dans le carré d’intérêt.
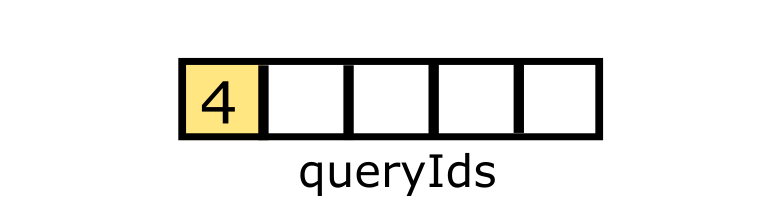
Pour finir, nous ajoutons la particule dans un tableau appelé queryIds pour l’utiliser plus tard dans l’application :On ajoute la particule dans un tableau qui s’appelle queryIds pour l’utiliser plus tard dans l’application :
Étape 3 : La confirmation de la collision
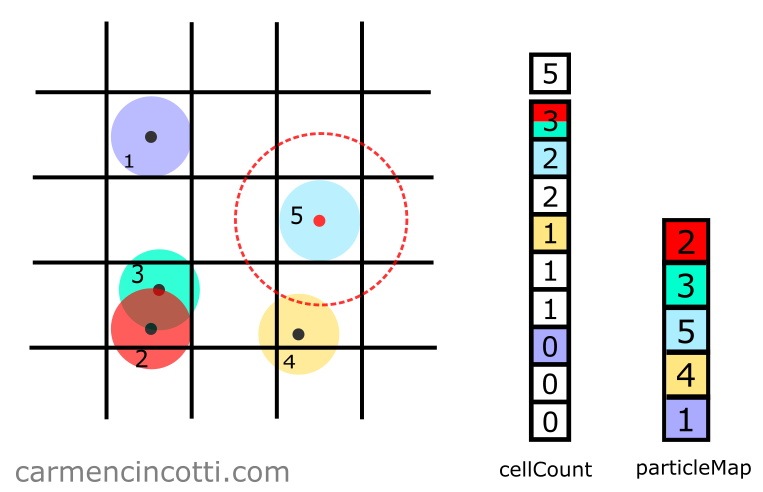
Avec notre tableau, queryIds, il est temps de confirmer que chaque particule trouvée lors de l’étape précédente se tombe dans la distance de recherche maximale, maxDist, de la particule d’intérêt, dans ce cas la particule :

On voit sur l’image ci-dessus que la particule se trouve bien dans ce rayon de recherche. Dans le code, nous devons utiliser une fonction de distance pour confirmer que c’est le cas. Nous pouvons utiliser une fonction de distance typique, comme ceci :
Si , on peut considérer que les deux particules se croisent !
Si , on remarquerait que les deux particules ne se croisent pas comme représenté sur l’image ci-dessous :
Bien sûr, nous pouvons éviter ces étapes en utilisant deux boucles pour visiter toutes les particules deux fois afin de déterminer si deux particules se croisent. Une telle opération aurait une complexité temporelle . Cependant, lors d’une simulation, une telle complexité n’est pas acceptable.
