Autocollisions de tissu | XPBD

La gestion des auto-collisions dans les simulations de tissus rendra une simulation beaucoup plus réelle. Cette semaine, nous étudierons quelques astuces que Matthias de Ten Minute Physics nous suggère d'utiliser pour nous aider à mettre cela en œuvre dans nos propres simulations.

Keywords: infographie, tutoriel, simulation de tissu, leetcode, autocollisions

By Carmen Cincotti

November 21, 2022

Qu’est-ce qu’une autocollision ?
Conseils pour l’implémentation des autocollisions
Des ressources (en français et anglais)

Autocollisions, dans une simulation de tissu, sont des collisions qui se produisent entre deux particules dans un morceau de tissu.

Jusqu’ici, nous avons développé une simulation d’un morceau de tissu qui vit dans GitHub.

La gestion des autocollisions dans notre simulation fait la différence entre une simulation qui semble réelle et une autre qui n’est pas vraiment impressionnante…

En suivant cet article, nous aurons une simulation capable de gérer des autocollisions comme celle-ci :

WebGPU Autocollisions d'un morceau de tissu pic.twitter.com/0uA5lBV2Ce
— Carmen Cincotti (@CarmenCincotti) November 15, 2022

Qu’est-ce qu’une autocollision ?

Une autocollision se produit lorsque deux particules internes d’un objet entrent en collision.

Particles colliding

En ce qui concerne un morceau de tissu, une autocollision se produit quand, par exemple, deux fils entrent en collision et ne se croisent pas, comme sur l’image ci-dessous :

Two threads crossing, which is incorrect. Another showing two threads not crossing, but instead colliding, which is correct behavior.

Les deux fils à gauche se croisent, ce qui n’est pas possible dans la vraie vie, car les fils obéissent aux lois de la physique. Les deux fils à droite nous montrent un comportement correct, car ils ne se croisent pas.

Conseils pour l’implémentation des autocollisions

Pour implémenter des autocollisions dans une simulation de tissu, j’expliquerai en détail cinq idées recommandées par Matthias de Ten Minute Physics.

Conseil 1 : Utiliser une table de hachage spatiale

Heureusement, nous avons déjà beaucoup parlé des tables de hachage spatiales !

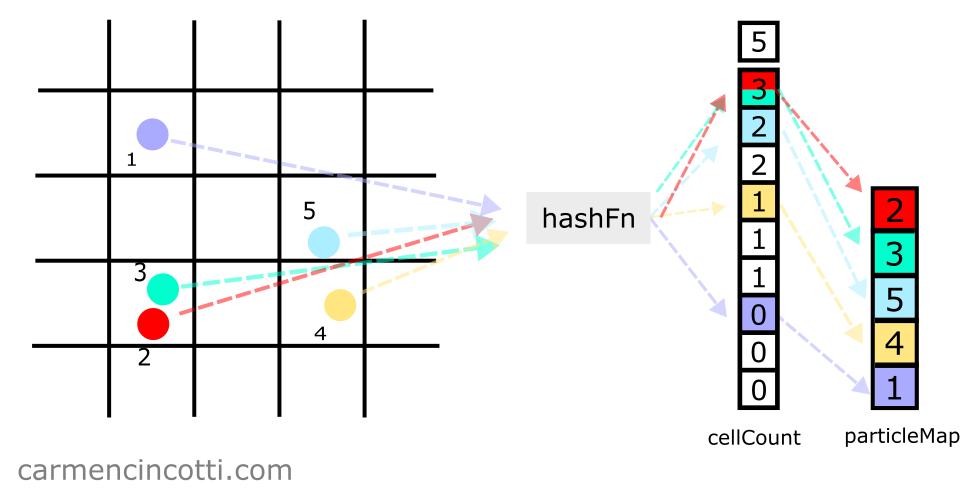
A hash table

Avec une table de hachage spatiale, nous pouvons détecter et corriger les collisions tout en bouclant la simulation XPBD.

Nous verrons le code d’une telle implémentation dans le prochain article.

Utiliser des particules uniformes

Cela dit, pour faciliter l’utilisation d’une table de hachage spatiale, il est recommandé d’utiliser des particules simples et uniformes.

Prenons l’image suivante ci-dessous comme exemple :

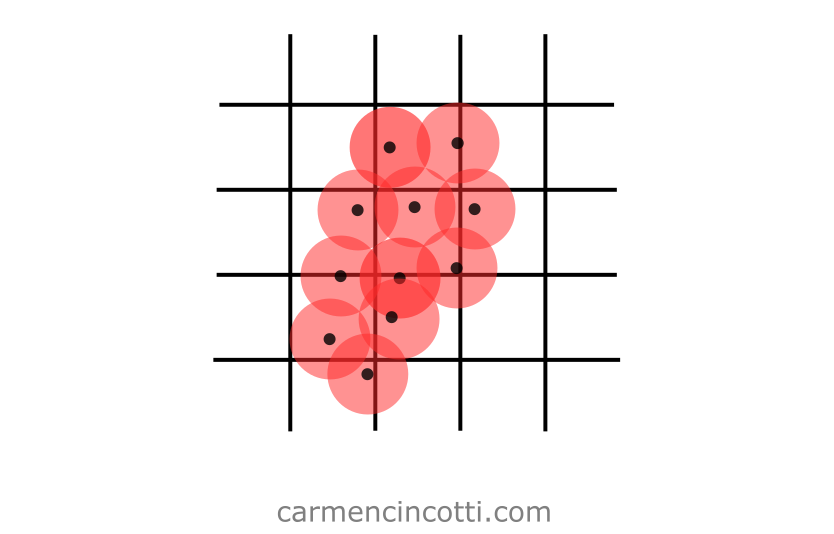
Les particules uniformes sont situées dans une table de hachage spatiale (qui est représentée sur l'image par la grille)

Les particules uniformes sont situées dans une table de hachage spatiale (qui est représentée par la grille sur l’image).

Avec cette approche, nous pouvons simplifier tous les calculs pour détecter les collisions entre les particules.

Voyons le cas inverse où les particules ne sont pas uniformes :

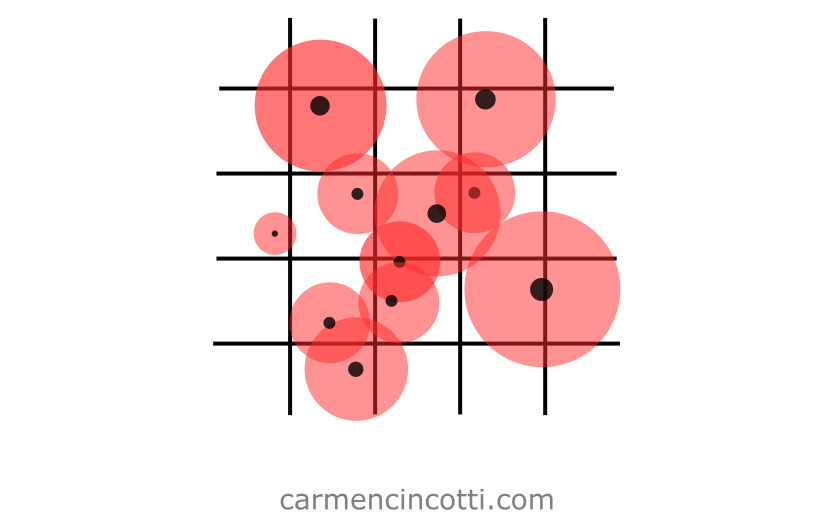
Non-uniform particles in a spatial hash map

En utilisant des particules non uniformes, nous devrons peut-être effectuer des calculs plus complexes pour détecter et corriger les collisions.

Conseil 2 : Éviter les simulations saccadées

Afin d’avoir une simulation de tissu visuellement agréable qui prend en compte les autocollisions, nous devons considérer attentivement les valeurs des deux paramètres suivants :

Longueur de repos entre les particules
Espacement entre les cellules dans une table de hachage spatiale

Pourquoi doit-on considérer tous les deux ?

Si ceux-ci sont mal configurés, il peut être impossible d’atteindre une simulation de tissu stable. En gros, ces deux paramètres sont liés.

Avant de voir pourquoi cela est le cas, passons en revue chaque paramètre.

Longueur de repos entre les particules

Rappelons que lors d’une simulation de tissu XPBD, nous définissons une longueur de repos entre les particules :

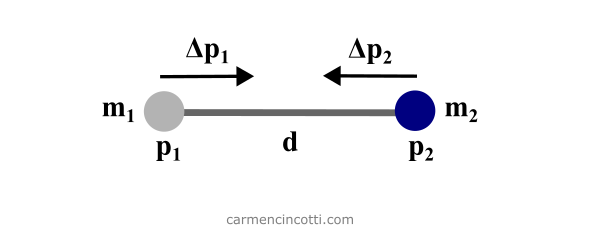
Distance constraint of a simulation XPBD

Sur l’image ci-dessus, la variable $d$ s’agit de la longueur de repos.

En termes de simulation XPBD, la longueur de repos, $d$ , entre deux particules agit comme une contrainte de distance, qui contraindra le mouvement des particules pendant une simulation afin de satisfaire la contrainte elle-même.

Espacement de la table de hachage spatiale

L’espacement est la taille de chaque cellule, ou “carré”, d’une table de hachage spatiale qui est représentée par la grille imaginaire dans l’image ci-dessous :

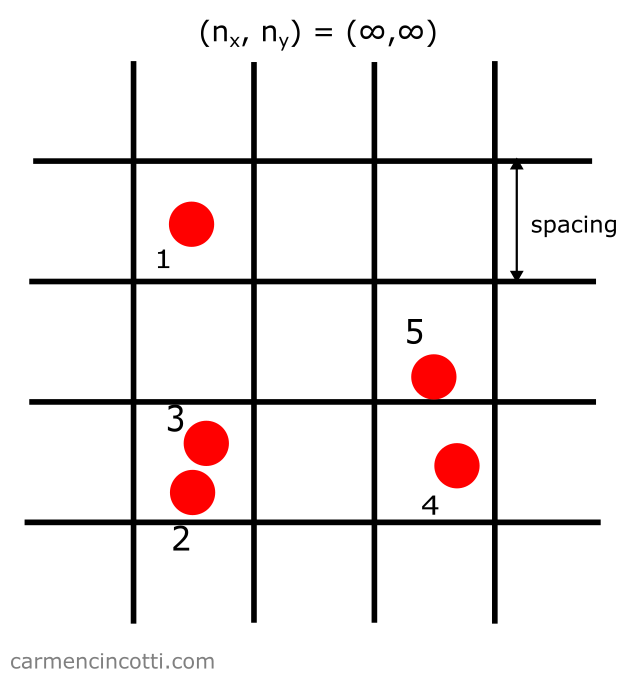
Spatial hash map represented by a grid that has a spacing parameter

Ce paramètre agit comme la distance minimale nécessaire entre deux particules pour ne pas être considérée comme une collision, $d_{coll}$ .

Le problème de l’instabilité

Imaginons que je souhaite créer une simulation avec seulement deux particules. Je définis d’abord la position initiale et le rayon, $r_p = 0.5$ des particules.

Ensuite, je définis nos deux paramètres d’intérêt :

La longueur de repos : $d_{rest} = 2.0$
Espacement : Deux fois le rayon d’une particule, $d_{coll} = 2r_p = 1.0$ .

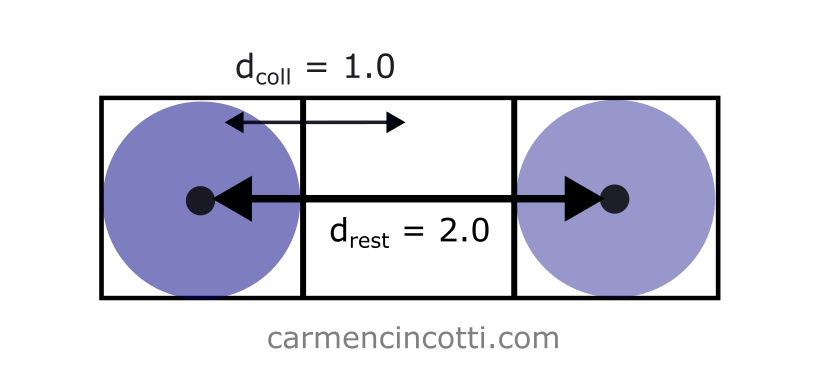
Params of an XPBD simulation set correctly

Dans ce cas, il n’y a pas de problème, car la longueur de repos est suffisamment longue pour que $d_{coll} < d_{rest}$ . Cela signifie que la contrainte de distance et la contrainte d’autocollision ne vont pas se battre pendant qu’elles tenteront de se résoudre.

Cependant, si j’avais défini $d_{rest} = 0.5$ … cela poserait des problèmes :

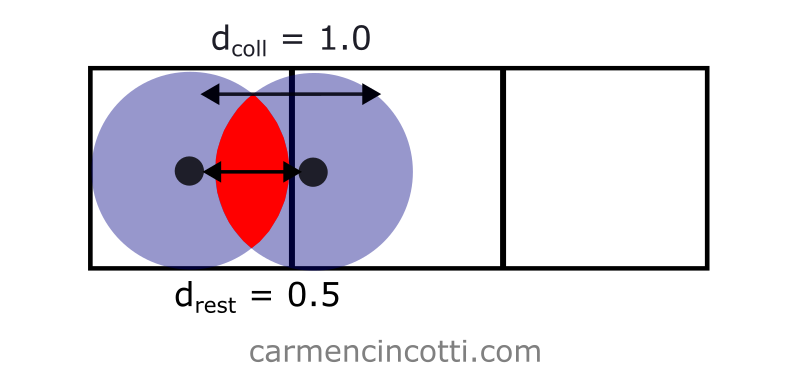
Params of an XPBD simulation not set correctly

Lors d’une telle simulation, la contrainte de distance tentera de se résoudre en rapprochant les particules les unes des autres.

Cependant, la contrainte d’autocollision tentera de se résoudre en agissant contre ce mouvement.

Cela provoquera une simulation très saccadée !

La solution

Pour éviter une simulation saccadée, il faut qu’on définisse $d_{coll}$ comme ceci :

d_{coll} = \text{min}(2r_{p}, d_{rest})

En définissant $d_{coll}$ comme ceci, la contrainte de distance et la contrainte de collision ne se combattront plus pour se résoudre.

Cela dit, lors d’une simulation de tissu, je propose de définir $d_{coll} = 2r_{p}$ et $d_{rest} > 2r_p$

Conseil 3 : Utiliser des sous-pas

Nous avons déjà appris de l’implémentation des sous-pas pour augmenter la stabilité d’une simulation XPBD il y a quelques mois. Nous pouvons également l’utiliser pour mieux détecter et corriger les collisions entre particules:

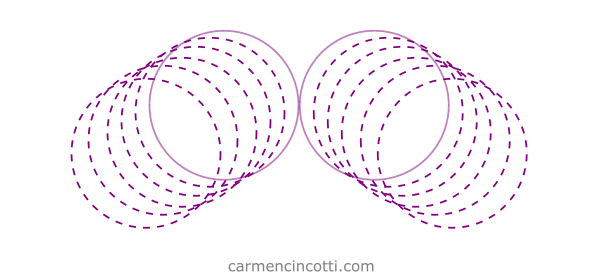
Collision between two particles, with substeps

Rappelons que pour implémenter cela, nous devons simplement diviser le pas de temps, $\Delta t$ , par le nombre de sous-pas souhaités, $n$ .

Ensuite, nous suivrons la simulation XPBD comme suit :

∆𝑡ₛ ← ∆𝑡/𝑛 (substep)
for all vertices i 
    initialize xᵢ = xᵢ_₀, vᵢ = vᵢ_₀, wᵢ = 1/mᵢ
while simulating
    createHash()
    for 𝑛 sub-steps
        for all particles 𝑖 (pre-solve)
            𝐯ᵢ ← 𝐯ᵢ + ∆𝑡ₛ*wᵢfₑₓₜ(𝐱ᵢ)
            𝐩ᵢ ← 𝐱ᵢ
            𝐱ᵢ ← 𝐱ᵢ + ∆𝑡ₛ*𝐯ᵢ
        for solverIterationCount
            for all constraints 𝐶 (solve)
                solve(𝐶, ∆𝑡ₛ) (solve for 𝐱ᵢ)
        for all particles 𝑖 (post-solve)
            𝐯ᵢ ← (𝐱ᵢ − 𝐩ᵢ)/∆tₛ
    render()

Cette fonctionnalité dans notre simulation nous permet d’éviter un système de détection de collision plus complexe comme la détection continue de collision (DCC). Pour en savoir plus, consultez cette ressource !

Conseil 4 : Limiter la vitesse

Jusqu’ici, nous avons beaucoup de moyens d’assurer une bonne simulation. Un problème qui reste cependant est le cas où les particules de la simulation se bougent trop rapidement, ce qui peut actualiser un phénomène qui s’appelle le tunneling :

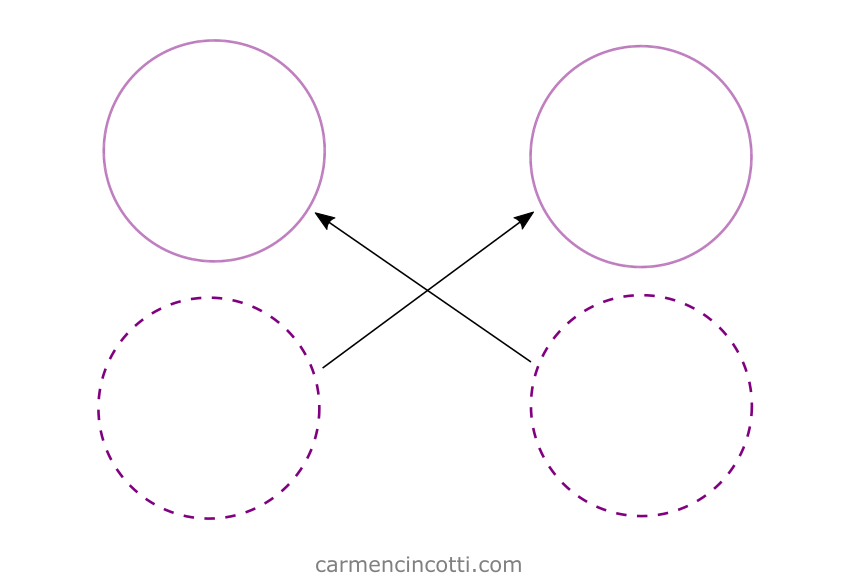
Two particles missing each other curing collision

Sur l’image, on voit deux particules qui devaient entrer en collision pendant ce pas de temps…

Cependant, ils se sont traversés !

Un levier que nous pouvons tirer pour éviter un tel comportement est de limiter la vitesse maximale de chaque particule.

Matthias de Ten Minute Physics nous recommande d’utiliser cette équation afin de trouver la vitesse maximale permise :

\mathbf{v}_{max} = \frac{r * n_{substeps}}{\Delta t}

où $r$ est le rayon d’une particule.

Nous pouvons constater dans cette équation que plus le nombre de sous-pas, $n$ que nous utilisons, plus la vitesse maximale permise s’augmente !

Prenons un exemple où j’ai un morceau de tissu contenant des particules avec des rayons de taille $\text{10cm}$ . Notre simulation s’exécute avec un pas de temps $\Delta t = \frac{1}{60}$ et des sous-pas $n = 20$ :

\mathbf{v}_{max} = \frac{\text{10cm} * 20}{\frac{1}{60}}\\[6px] \mathbf{v}_{max} = 120\frac{\text{m}}{\text{s}}

En utilisant l’équation ci-dessus, nous calculons une vitesse maximale autorisée de $120\frac{\text{m}}{\text{s}}$ … ce qui est très rapide ! Dans une simulation de tissu, nous n’arriverons probablement jamais à dépasser une vitesse aussi élevée.

Voyons un autre exemple avec moins de sous-étapes et un pas de temps plus grand : $n = 1$ et $\Delta t = \frac{1}{30}$ :

\mathbf{v}_{max} = \frac{\text{10cm} * 1}{\frac{1}{30}}\\[6px] \mathbf{v}_{max} = 3\frac{\text{m}}{\text{s}}

Nous avons calculé une vitesse maximale de $3\frac{\text{m}}{\text{s}}$ , soit la vitesse d’un humain qui marche !

Nous pouvons raisonnablement croire que les particules d’une simulation de tissu pourraient se déplacer plus rapidement que cela.

Donc, pour éviter tout problème potentiel avec le tunneling, nous devons limiter la vitesse des particules pour ne pas dépasser ce seuil de vitesse maximale.

Conseil 5 : Introduire de la friction

Enfin, il est recommandé par Matthias d’introduire la friction lors de nos calculs afin de mieux stabiliser la simulation lors d’une collision.

Il faut l’introduire lors de la boucle du solveur de contraintes, plus précisément en suivant le calcul et la correction positionnelle d’une particule qui vient d’entrer en collision avec une autre particule.

Comment calculer la correction de friction

Imaginons que nous venons de calculer les nouvelles positions $x_1, x_2$ de deux particules qui viennent de se heurter. L’étape suivante consiste à calculer la vitesse de chaque particule en utilisant l’intégration par Verlet.

\mathbf{v_1} = (\mathbf{x_1} - \mathbf{p_1}) / h \\[6pt] \mathbf{v_2} = (\mathbf{x_2} - \mathbf{p_2}) / h \\[6pt]

Ensuite, nous calculons la vitesse moyenne.

\mathbf{v_{avg}} = (\mathbf{v_1} - \mathbf{v_2}) / 2 \\[6pt]

Ensuite, on trouve la différence entre $\mathbf{v_{avg}}$ et chaque vitesse déjà calculée $\mathbf{v_{2}}, \mathbf{v_{1}}$ :

\Delta {\mathbf{v}_1} = \mathbf{v_{avg}} - \mathbf{v_{1}}\\[6pt] \Delta {\mathbf{v}_2} = \mathbf{v_{avg}} - \mathbf{v_{2}}\\[6pt]

Enfin, les positions sont mises à jour en ajoutant $\Delta \mathbf{v}_i * d$ , où $d$ est un facteur de damping qui est entre $0$ et $1$ :

\mathbf{x_1} \leftarrow \mathbf{x_1} + (d * \Delta {\mathbf{v}_1}) * h \\[6pt] \mathbf{x_2} \leftarrow \mathbf{x_2} + (d * \Delta {\mathbf{v}_2}) * h \\[6pt]

Je ne comprends pas le raisonnement derrière l’utilisation de la vitesse moyenne pendant ces étapes… alors si vous savez, contactez-moi !

Carmen's Graphics Blog