Continuons notre conversation sur le tissu après avoir déjà parlé des matériaux utilisés pour le fabriquer. Bien que chaque morceau de tissu soit différent, nous pouvons modéliser les structures internes de la même manière.

Selon les articles scientifiques, le tissu peut être modélisé de manière continue ou de manière discrète. Lors de cet article, on se concentre sur la représentation discrète parce que l’on connait déjà ce que sont les * systèmes masse-ressorts** ⚖️.

Avec ce choix, nous verrons comment modéliser du tissu dans un environnement 3D - y compris l’utilisation de triangles, particules et forces.

Modélisation - continue contre discrète

Nous devons d’abord choisir comment modéliser notre tissu, car cela influencera toute notre simulation ! La plupart des recherches modélisent le tissu comme un matériau continu ou discret.

Continue

Une représentation continue du tissu ignore le fait qu’il y a des atomes et des trous entre les fils (entre les chaînes et les trames). En d’autres termes, le tissu est comme un seul corps où une force ou une déformation agit entièrement sur ce corps. Par conséquent, si je choisis un point n’importe où sur le tissu, il pourrait exister, car il n’y a pas de discontinuités.

Cette approche ouvre la porte à l’utilisation de la mécanique des milieux continus pour simuler notre tissu, qui est décrit par Wikipédia comme suit :

La mécanique des milieux continus est le domaine de la mécanique qui s’intéresse à la déformation des solides (continus).

Cette branche de la mécanique permet une simulation plus authentique et réaliste. Cependant, les calculs sont chers et complexes à cause des systèmes d’équations aux dérivées partielles ! 🧮

En plus, lors de la simulation, il serait nécessaire de discrétiser notre modèle en temps et en espace. Pour ce faire, on utilise généralement une discrétisation par éléments finis en utilisant la méthode des éléments finis (MEF).

L’idée de MEF est de discrétiser, ou mailler, une surface continue en éléments simples, ou maillages.

Discret

Une représentation discrète est basée sur le fait qu’un morceau de tissu n’est pas du tout continu.

D’après notre conversation de la semaine dernière, nous savons que le tissu est composé de fils qui se croisent (chaînes et trame). Ainsi, si on zoome sur un morceau de tissu, on verra sa véritable structure 🧵 :

Au fur et à mesure que le tissu bouge, les fils entrent en collision, se plient, etc. en raison de l’entrelacement des chaînes et des trames. Il est donc possible de modéliser les fils comme des éléments discrets individuels. Cependant, la modélisation de tous ces éléments discrets est complexe et peu pratique.

Dans ce cas, les chercheurs scientifiques recommandent une représentation particulaire :

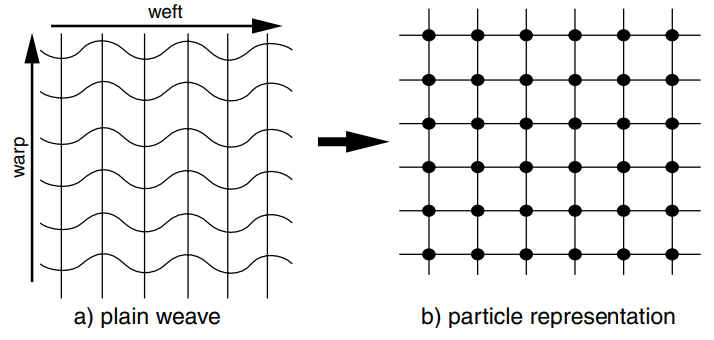
Cette représentation fait un zoom sur l’élément discret - la particule - qui représente un point de croisement entre une trame et une chaîne. Les interactions mécaniques (les forces d’étirement, de compression, de flexion, et de torsion) sont calculées à partir des relations entre particules locales voisines.

La représentation discrète du tissu

Je choisis d’avancer avec une représentation discrète du tissu, car nous avons déjà implémenté un système de particules dans le passé. Alors, plongeons un peu plus dans ce type de représentation.

Triangles

Notre modèle du tissu sera un maillage triangulaire, où chaque sommet sera notre représentation d’une particule. Voici cet exemple :

par Obi

Les points bleus visibles sur le tissu sont des particules dans ce maillage ! Le tissu que je viens de créer dans Blender est proche de cette idée :

Lorsque je l’exporterai, je choisirai de trianguler le maillage pour m’assurer que je bosse avec des triangles.

Particules

Le comportement des particules est gouverné par les lois de la physique qui décrivent les propriétés des matériaux. Autrement dit, les particules doivent réagir aux forces qui agissent sur elles.

Pour ce faire, il faut que la position et la vitesse des particules changent dans le temps. La combinaison de la position et de la vitesse dans une structure de données est appelée espace de phase. On a déjà vu cette représentation des particules il y a quelques mois lors de l’article sur la création d’un système des particules.

La masse

Dans la partie suivante, nous allons voir que les particules font partie d’un système masse-ressort. Cela dit, comment est-ce qu’on détermine la masse d’une particule donnée ? 🤔

Vu que le tissu est formé par un maillage de triangles, une option pour calculer la masse est de définir d’abord une densité pour le tissu. Rappelons que l’unité de la densité est kg / m². Il faut donc trouver l’aire d’un triangle pour trouver sa masse. Enfin, on divise cette masse totale par trois afin de trouver la masse d’un sommet.

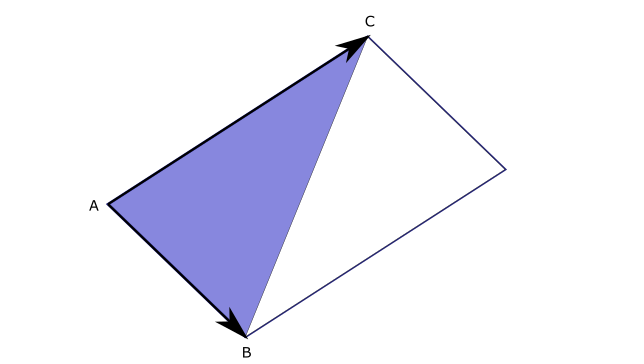
Voyons une astuce pour trouver l’aire d’un triangle en utilisant le produit croisé. L’amplitude du produit u × v est par définition l’aire du parallélogramme. Par conséquent, nous pouvons utiliser le produit croisé pour calculer l’aire d’un triangle formé par trois points A, B et C dans l’espace.

Supposons que nous connaissions la position de chaque sommet. Il est ainsi possible de résoudre l’aire comme suit :

Les forces

Bien qu’il y ait des forces externes qui affectent le tissu comme la gravité, le vent et les collisions avec d’autres corps, les forces internes sont responsables du comportement du tissu que nous le connaissons.

Les forces internes d’intérêt qui agiront sur les particules de notre modèle sont l’étirement (stretch), la flexion (bend) et le cisaillement (shear). L’idée est que ces forces feront bouger les particules d’une manière similaire à la façon dont un tissu se déforme et se drape.

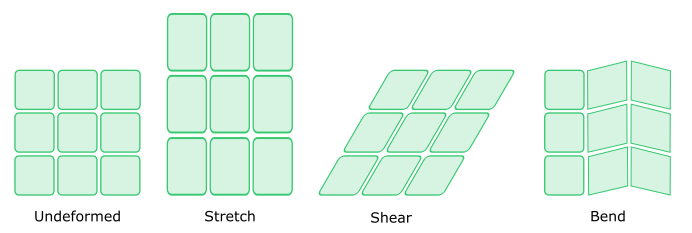
Le processus de simulation de telles forces est le même que la simulation 2D que nous avons faite ensemble il y a quelques mois.

Nous pouvons modéliser les interactions entre les particules comme un système masse-ressort. Voici un exemple d’un tel système :

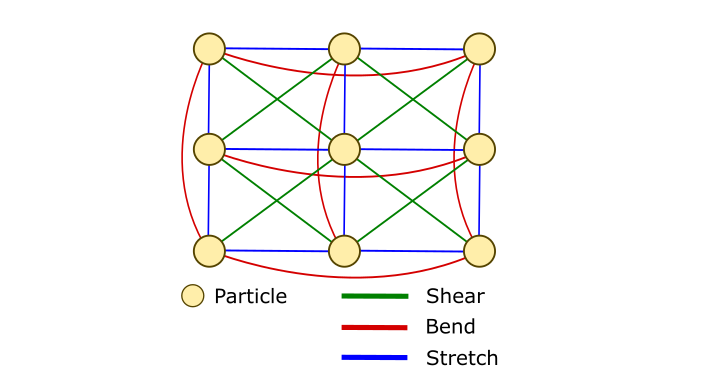
Il suffit de calculer la position et la vitesse de chaque particule après avoir pris en compte toutes les forces. Nous devons utiliser une méthode numérique pour résoudre ce système comme nous l’avons déjà vu dans un article précédent - Méthode d’Euler implicite.

En tout cas, il faut choisir la méthode numérique qui répond à vos besoins.

La suite

Nous allons tirer parti de ces connaissances et approfondir une manière potentielle de résoudre cette simulation de tissu, avec une dynamique basée sur la position (position based dynamics - PBD).

Des ressources (en français et anglais)

• A Consistent Bending Model for Cloth Simulation with Corotational Subdivision Finite Elements - B. Thomaszewski, M. Wacker, W. Straßer
• Efficient cloth simulation using an adaptive finite element method - J. Bender, C. Deul
• Realistic Cloth Animation - J. Cordero
• Discrete and Continuous Simulation
• Basics of Continuum Mechanics - ETH
• The vector product - The University of Sydney