La boucle de simulation | PBD

La dynamique basée sur la position est une technique de simulation rapide, stable et contrôlable qui manipule directement les positions des sommets des maillages d'objets afin de modéliser divers effets dynamiques et interactifs d'objets tels qu'un corps rigide, un corps mou, un tissu ou des fluides. Voyons sa boucle de simulation pour mieux comprendre comment cela fonctionne.

Keywords: physique, dynamique, algèbre linéaire, calcul à plusieurs variables, gradient, linéarisation

By Carmen Cincotti

August 01, 2022Updated September 12, 2022

L’algorithme de la dynamique basée sur la position (PBD)
La boucle
Prochainement…
Des ressources (en français et anglais)

Nous sommes sur le point de comprendre presque tout sur la dynamique basée sur la position (PBD). En lisant ces deux articles sur PBD et son successeur XPBD, j’ai vite réalisé qu’il y avait de nombreux concepts qui m’étaient totalement inconnus. Alors, j’ai encore une fois décidé d’écrire à leur sujet.

J’écrirai cette semaine sur la boucle de simulation de PBD, ligne par ligne, afin de mieux la comprendre tout cela. Dans le prochain article, j’écrirai sur le successeur de PBD, XPBD. À la fin, je choisirai entre PBD et XPBD comme boucle de simulation pour passer à la mise en place d’une simulation de tissu.

L’algorithme de la dynamique basée sur la position (PBD)

Voici l’algorithme pour exécuter une simulation avec PBD :

L'algorithme de simulation de PBD

Figure 1 : L’algorithme de simulation de PBD - J. Bender, M. Müller and M. Macklin / A Survey on Position Based Dynamics, 2017

Les lignes (1)-(3) servent à initialiser la position et la vitesse des particules, car le système est du second ordre par rapport au temps : $\mathbf{x_{n+1}} = \mathbf{x_n} + \mathbf{v_n} \Delta t + w \mathbf{f} \Delta t^2$ . Sinon, il y aurait trop de variables inconnues.

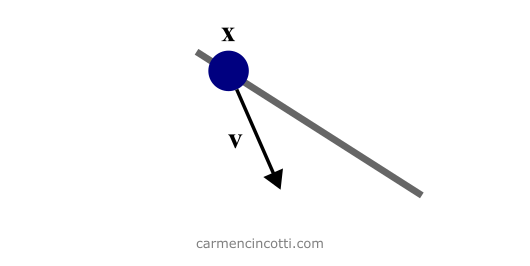
Initialisation de PBD. La particule x est contrainte à la ligne (en gris). Il a une vitesse de vecteur v

Figure 2 : Initialisation de PBD. La particule x est contrainte à la ligne (en gris). Il a une vitesse de vecteur v.

Rappelons que PBD travaille exclusivement et directement sur les positions des particules dans un système. Il n’est donc pas nécessaire de maintenir la couche d’accélération pour calculer la vitesse et donc la position dans les étapes futures.

La boucle

On entre maintenant dans la boucle de simulation ! À chaque itération, on prend un pas dans le temps, $\Delta t$ pour faire avancer la simulation.

Les lignes (5)-(6) (de Figure 1) effectuent une étape d’intégration d’Euler symplectique pour faire avancer la position et la vitesse. Le nouvel emplacement, $\mathbf{p_i}$ est juste une prédiction de la position finale de la particule non soumise à aucune contrainte. Nous ne considérons les contraintes que plus tard.

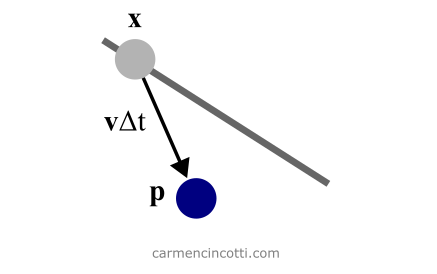
La prédiction de la position x de la particule.

Figure 3 : La prédiction de la position x de la particule. La prédiction est représentée par une deuxième variable temporaire p.

L’intégration d’Euler symplectique

L’intégration typique d’Euler fait avancer un système dans le temps $\Delta t$ , ou appelé $h$ ici, comme suit :

\mathbf{x_{n+1}} = \mathbf{x_n} + h \mathbf{v_n} \\[6pt] \mathbf{v_{n+1}} = \mathbf{v_n} + h \frac{1}{m} \mathbf{f_n}

Notez bien que la vitesse $\bf{v}$ est mise à jour après la mise à jour de la position $\bf{x}$ . Cependant, cette méthode augmente l’énergie potentielle du système qu’elle simule. Pour lutter contre cela, on utilise l’intégration d’Euler symplectique :

\mathbf{v_{n+1}} = \mathbf{v_n} + h \frac{1}{m} \mathbf{f_n} \\[6pt] \mathbf{x_{n+1}} = \mathbf{x_n} + h \mathbf{v_{n+1}}

Nous déterminons d’abord la vitesse du système dans le pas de temps désigné, $h$ , puis utilisons cette nouvelle vitesse pour calculer la position.

Voici cette vidéo pour en savoir plus :

À la ligne (7), on continue avec la génération des contraintes externes non permanentes telles que les contraintes de collision. Nous devons les générer à ce moment précis pour effectuer la détection de collision continue avec la nouvelle position prédite, $\mathbf{p}$ , de l’étape précédente. Je reviendrai sur le sujet des collisions dans un article ultérieur.

Le solveur de Gauss—Seidel “non linéaire”

Pendant les lignes (8)-(10), un solveur corrige itérativement les positions prédites, $\mathbf{p}$ afin de satisfaire les contraintes définies dans le système.

Dans l’article A Survey on Position Based Dynamics, 2017 - Jan Bender , Matthias Müller et Miles Macklin, il y a cette idée d’un solveur Gauss—Seidel non-linéaire, car Gauss-Seidel est généralement utilisé pour résoudre des systèmes linéaires. Rappelons que la différence entre les contraintes linéaires et non linéaires est la suivante :

Linéaire - Les contraintes d’inégalité linéaires ont la forme $A·x ≤ b$ . Les contraintes d’égalité linéaires ont la forme $A·x = b$ .
Non linéaire - Les contraintes d’inégalité non linéaires ont la forme $c(x) ≤ 0$ . De même, les contraintes d’égalité non linéaires ont également la forme $c(x) = 0$ .

La méthode de Gauss—Seidel

On utilise la méthode de Gauss—Seidel pour résoudre un système d’équations linéaires. Rappelons qu’une équation linéaire prend la forme :

A\mathbf{x} = \mathbf{b}

Notez bien que cette méthode numérique est itérative. Autrement dit, on utilise une boucle pour approcher itérativement une solution approximée… ce qui m’a fait réfléchir. Pourquoi dois-je utiliser une méthode numérique pour résoudre une équation comme $A\mathbf{x} = \mathbf{b}$ ? Voici une excellente ressource (diapositive 2) qui répond à cette question.

En regardant cet exemple de la méthode en action - on voit ce qui est particulièrement intéressant sur cette méthode. Nous remplaçons les anciennes valeurs par nos toutes nouvelles valeurs calculées numériquement à chaque itération.

En appliquant ces connaissances concernant la satisfaction des contraintes dans le système, on voit que chaque équation contrainte sera résolue individuellement et le résultat de l’une sera immédiatement impliqué dans le calcul de l’autre. Cependant, notre système n’a qu’une seule contrainte pour être plus simple comme exemple. Imaginons que s’il y en avait deux que lors d’une itération, le résultat de l’un influencerait immédiatement le résultat des autres.

Dans tous les cas, le but est de résoudre les contraintes comme dans cette image ci-dessous :

L'algorithme de Gauss—Seidel en action.

Figure 4 : L’algorithme de Gauss—Seidel en action. La position prédite p est déplacée pour satisfaire la contrainte (la ligne grise).

Plus précisément, nous souhaitons mettre itérativement à jour $\mathbf{p}$ pour satisfaire nos contraintes :

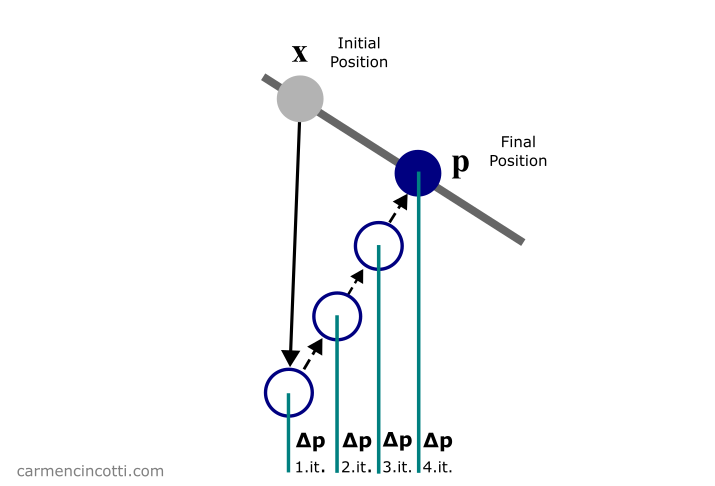
Iteration of Gauss-Seidel

Figure 5: La position prédite p est déplacé itérativement de $\Delta \mathbf{p}$ pour satisfaire la contrainte (la ligne grise).

Génial ! Nous avons un solveur prêt à nous aider à résoudre le système 🎉 ! Cependant, nous avons une petite question à laquelle nous devons répondre 🤔 :

Comment trouver $\Delta \mathbf{p}$ ?

Corriger la position des particules avec la méthode de Newton Raphson

Pour trouver le déplacement de la particule $\Delta \mathbf{p}$ , nous utiliserons un processus basé sur la méthode de Newton-Raphson.

La méthode de Newton—Raphson

Le but de la méthode de Newton—Raphson est de déterminer itérativement les racines d’une fonction arbitraire et non linéaire. Autrement dit, on minimise cette fonction (supposons une fonction $f(x)$ ) en trouvant la valeur de $x$ qui fera $f(x) = 0$ .

Prenons par exemple cette fonction $f(x) = 0.1x^2 - 1$ . On commence par supposer que la valeur $x = 6$ minimisera la fonction. On trace une droite tangente à la courbe $f(x)$ comme ceci :

Graph of equation 0.1 x squared minus one - first attemp

C’est clair que $f(x)$ n’est pas minimisé par $x = 6$ , car $f(6) = 3.833$ . Nous continuons à chercher des racines en réessayant à $x = 3.833$ :

Graph of equation 0.1 x squared minus one - second attempt

Enfin, on répète ce processus pour enfin trouver la racine $(3.1623, 0)$ .

Regardez cette vidéo pour en savoir plus

En suivant la méthode de Newton-Raphson, nous voulons linéariser les fonctions de contrainte. Dans le cas d’une contrainte d’égalité, elle est approximée en la linéarisant comme suit :

C(\mathbf{x} + \Delta \mathbf{x}) \approx C(\mathbf{x}) + \nabla C(\mathbf{x}) \cdot \Delta \mathbf{x} = 0

Pour maintenir le moment linéaire et angulaire, on restreint $\Delta \mathbf{p}$ dans la direction de $\nabla C$ :

\Delta \mathbf{p} = \lambda \mathbf{M}^{-1} \nabla C \mathbf{p}^T

où $\mathbf{M}$ est les masses des particules (on les inverse pour pondérer les corrections proportionnelles aux masses inverses). À première vue, je me suis dit : euh, quoi ? Cependant, j’ai créé quelques graphiques pour au moins clarifier cette équation (même si je suis encore perdu sur la conservation des moments).

Imaginons qu’il y a une fonction contrainte $C(x) = -x - y$ . L’idée est que nous voulons qu’un point arbitraire reste sur cette ligne indépendamment des forces externes :

Constraint chart

Nous voulons minimiser $C(x) = 0$ . Pour ce faire, on voyage dans le sens du gradient de $C(\mathbf{x})$ , $\nabla C(\mathbf{x})$ :

Contraints with gradients

Si je place arbitrairement un point $\mathbf{x}$ sur ce graphique et ensuite j’aimerais que le point reste toujours sur $C(\mathbf{x})$ - il est logique que je le fasse voyager dans la direction du gradient de $C(\mathbf{x})$ pour revenir le plus vite possible à la ligne !

Constraints with gradients and example point

Notre prochaine étape consiste à trouver la valeur de notre multiplicateur de Lagrange (un facteur scalaire) $\lambda$ et puis à calculer $\Delta \mathbf{p}$ . La réécriture de l’approximation linéaire de $C(\mathbf{x})$ est la suivante :

- C(\mathbf{p}) = \nabla C(\mathbf{p}) \cdot \Delta \mathbf{p} \\[6pt]

où

\Delta \mathbf{p} = \lambda \mathbf{M}^{-1} \nabla C \mathbf{p}^T

On peut effectuer une substitution pour trouver $\lambda$ :

\lambda = \frac{C(\mathbf{x})}{\nabla C(\mathbf{x})\mathbf{M}^{-1}\nabla C(\mathbf{x})^T} \\[6pt] \lambda = \frac{C(\mathbf{x})}{|\nabla C(\mathbf{x})|^2 \mathbf{M}^{-1}}

Après avoir enfin trouvé $\lambda$ et par conséquent $\Delta \mathbf{p}$ , on met à jour $\mathbf{p}$ .

\mathbf{p_{new}} = \mathbf{p} + \Delta \mathbf{p}

Rappelons que $\mathbf{p}$ est une variable de position temporaire. On met à jour notre variable de position originale $\mathbf{x}$ dans l’étape suivante.

Ensuite, nous passons par une autre itération du solveur “non linéaire” de Gauss-Seidel.

La mise à jour finale avec l’intégration de Verlet

Pendant les lignes (10)-(12) - après le solveur de Gauss-Seidel, on met à jour la position et la vitesse de chaque particule à l’aide d’une méthode d’intégration qui s’appelle intégration de Verlet :

\mathbf{v_i} = \frac{\mathbf{p_i} -\mathbf{x_i}}{\Delta t}\\[6pt] \mathbf{x_i} = \mathbf{p_i}

Avec l’intégration de Verlet - au lieu de stocker la position et la vitesse de chaque particule, nous stockons sa nouvelle position $\mathbf{p_i}$ et sa position précédente $\mathbf{x_i}$ . Comme vous pouvez le voir, avec eux, nous pouvons calculer la nouvelle vitesse, $\mathbf{v_i}$ !

Ensuite, la boucle recommence et nous recommençons tout le processus ! 🎉

Prochainement…

PBD peut être étendu pour fournir des simulations plus agréables visuellement par son successeur XPBD. Nous verrons cela dans le prochain article !

Carmen's Graphics Blog