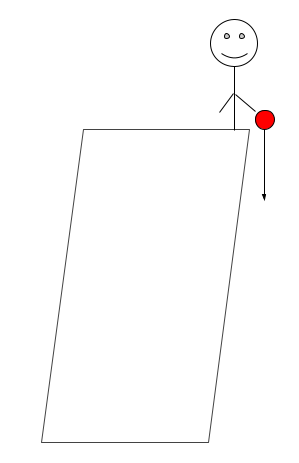
This week, I continued my studies on classical mechanics and how one can derive equations of motion. I ended up finding a pretty easy problem described below (this is an example found in No-Nonsense Classical Mechanics ):
I’m on the Tower of Pisa and I drop a ball straight down. I would like to calculate the equation of motion describing the free fall of the ball towards the ground:
To find this, we can use three different methods. These methods are:
Newton’s method
The Lagrange method
Hamilton’s method
We start with Newton’s second law :
F ⃗ = m a ⃗ = d p ⃗ d t p ⃗ = m v ⃗ \vec{F} = m\vec{a} = \dfrac{d\vec{p}}{dt} \\
\vec{p} = m\vec{v} \\ F = m a = d t d p p = m v where F a p t
Knowing this law, we can rewrite the equation like so:
F ⃗ = d ( m v ⃗ ) d t = m ( v x v y v z ) d d t \vec{F} = \dfrac{d(m\vec{v})}{dt} = m\begin{pmatrix} v_{x} \\ v_{y} \\ v_{z} \end{pmatrix} \dfrac{d}{dt} \\ F = d t d ( m v ) = m ⎝ ⎛ v x v y v z ⎠ ⎞ d t d Neglecting wind resistance, and assuming the point where we drop the ball is the origin, we can see that the only driving force is gravity:
F ⃗ = ( 0 0 − m g ) \vec{F} = \begin{pmatrix} 0 \\ 0 \\ -mg \end{pmatrix} \\ F = ⎝ ⎛ 0 0 − m g ⎠ ⎞ which is equivalent to:
∴ d ( m v ⃗ ) d t = ( 0 0 − m g ) \therefore \frac{d(m\vec{v})}{dt} = \begin{pmatrix} 0 \\ 0 \\ -mg \end{pmatrix} ∴ d t d ( m v ) = ⎝ ⎛ 0 0 − m g ⎠ ⎞ We can now solve the equation of motion:
∫ 0 t ( 0 0 − g ) d t = ∫ 0 t d d t ( v x v y v z ) d t ∵ ∫ a b d f d t d t = f ( b ) − f ( a ) ( 0 0 − g t ) = ( v x ( t ) v y ( t ) v z ( t ) ) − ( v x ( 0 ) v y ( 0 ) v z ( 0 ) ) ∫ 0 t ( 0 0 − g t ) d t = ∫ 0 t ( ( v x ( t ) v y ( t ) v z ( t ) ) − ( v x ( 0 ) v y ( 0 ) v z ( 0 ) ) ) d t ( 0 0 − 1 2 g t 2 ) = ( x x ( t ) x y ( t ) x z ( t ) ) − ( x x ( 0 ) x y ( 0 ) x z ( 0 ) ) − ( v x ( 0 ) ( t ) v y ( 0 ) ( t ) v z ( 0 ) ( t ) ) + ( v x ( 0 ) ( 0 ) v y ( 0 ) ( 0 ) v z ( 0 ) ( 0 ) ) ∵ I n i t i a l c o n d i t i o n s : v ( 0 ) = ( 0 0 0 ) , x ( 0 ) = ( 0 0 0 ) ∴ ( 0 0 − 1 2 g t 2 ) = ( x x ( t ) x y ( t ) x z ( t ) ) \int_0^t \begin{pmatrix} 0 \\ 0 \\ -g \end{pmatrix} dt = \int_0^t \dfrac{d}{dt} \begin{pmatrix} v_{x} \\ v_{y} \\ v_{z} \end{pmatrix} dt\newline
\because \int_a^b \dfrac{df}{dt}dt = f(b) - f(a) \newline
\begin{pmatrix} 0 \\ 0 \\ -gt \end{pmatrix} = \begin{pmatrix} v_{x}(t) \\ v_{y}(t) \\ v_{z}(t) \end{pmatrix} - \begin{pmatrix} v_{x}(0) \\ v_{y}(0) \\ v_{z}(0) \end{pmatrix} \newline
\int_0^t \begin{pmatrix} 0 \\ 0 \\ -gt \end{pmatrix}dt = \int_0^t (\begin{pmatrix} v_{x}(t) \\ v_{y}(t) \\ v_{z}(t) \end{pmatrix} - \begin{pmatrix} v_{x}(0) \\ v_{y}(0) \\ v_{z}(0) \end{pmatrix}) dt \newline
\begin{pmatrix} 0 \\ 0 \\ -\dfrac{1}{2}gt^2 \end{pmatrix} = \begin{pmatrix} x_{x}(t) \\ x_{y}(t) \\ x_{z}(t) \end{pmatrix} - \begin{pmatrix} x_{x}(0) \\ x_{y}(0) \\ x_{z}(0) \end{pmatrix} - \begin{pmatrix} v_{x}(0)(t) \\ v_{y}(0)(t) \\ v_{z}(0)(t) \end{pmatrix} + \begin{pmatrix} v_{x}(0)(0) \\ v_{y}(0)(0) \\ v_{z}(0)(0) \end{pmatrix} \newline
\because Initial\ conditions:\ v(0) = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}, x(0) = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}
\\
\therefore \begin{pmatrix} 0 \\ 0 \\ -\dfrac{1}{2}gt^2 \end{pmatrix} = \begin{pmatrix} x_{x}(t) \\ x_{y}(t) \\ x_{z}(t) \end{pmatrix} ∫ 0 t ⎝ ⎛ 0 0 − g ⎠ ⎞ d t = ∫ 0 t d t d ⎝ ⎛ v x v y v z ⎠ ⎞ d t ∵ ∫ a b d t d f d t = f ( b ) − f ( a ) ⎝ ⎛ 0 0 − g t ⎠ ⎞ = ⎝ ⎛ v x ( t ) v y ( t ) v z ( t ) ⎠ ⎞ − ⎝ ⎛ v x ( 0 ) v y ( 0 ) v z ( 0 ) ⎠ ⎞ ∫ 0 t ⎝ ⎛ 0 0 − g t ⎠ ⎞ d t = ∫ 0 t ( ⎝ ⎛ v x ( t ) v y ( t ) v z ( t ) ⎠ ⎞ − ⎝ ⎛ v x ( 0 ) v y ( 0 ) v z ( 0 ) ⎠ ⎞ ) d t ⎝ ⎜ ⎜ ⎛ 0 0 − 2 1 g t 2 ⎠ ⎟ ⎟ ⎞ = ⎝ ⎛ x x ( t ) x y ( t ) x z ( t ) ⎠ ⎞ − ⎝ ⎛ x x ( 0 ) x y ( 0 ) x z ( 0 ) ⎠ ⎞ − ⎝ ⎛ v x ( 0 ) ( t ) v y ( 0 ) ( t ) v z ( 0 ) ( t ) ⎠ ⎞ + ⎝ ⎛ v x ( 0 ) ( 0 ) v y ( 0 ) ( 0 ) v z ( 0 ) ( 0 ) ⎠ ⎞ ∵ I n i t i a l c o n d i t i o n s : v ( 0 ) = ⎝ ⎛ 0 0 0 ⎠ ⎞ , x ( 0 ) = ⎝ ⎛ 0 0 0 ⎠ ⎞ ∴ ⎝ ⎜ ⎜ ⎛ 0 0 − 2 1 g t 2 ⎠ ⎟ ⎟ ⎞ = ⎝ ⎛ x x ( t ) x y ( t ) x z ( t ) ⎠ ⎞ Well, after seeing that it is possible to solve this problem with Newton’s method, let’s move on to Lagrange’s method.
In general, in Lagrangian mechanics, the Lagrangian is::
L ( q , q ˙ ) = T ( q ˙ ) − V ( q ) L(q, \dot{q}) = T(\dot{q}) - V(q) \\ L ( q , q ˙ ) = T ( q ˙ ) − V ( q ) where T V
T = 1 2 m v ⃗ 2 a n d V = m g z ∴ L = 1 2 m ( v x 2 + v y 2 + v z 2 ) − m g h T = \frac{1}{2}m\vec{v}^2\ and\ V = mgz \\
\therefore L = \frac{1}{2}m(v_x^2 + v_y^2 + v_z^2) - mgh \\ T = 2 1 m v 2 a n d V = m g z ∴ L = 2 1 m ( v x 2 + v y 2 + v z 2 ) − m g h Recall that the Euler-Lagrange equation is as follows:
∂ L ∂ q = d d t ( ∂ L ∂ v q ) \frac{\partial{L}}{\partial{q}} = \frac{d}{dt}(\frac{\partial{L}}{\partial{v_q}}) \\ ∂ q ∂ L = d t d ( ∂ v q ∂ L ) So we just need to rewrite the Euler-Lagrange equation using our variables:
∂ ( 1 2 m ( v x 2 + v y 2 + v z 2 ) ) − m g z ∂ x = d d t ∂ ( 1 2 m ( v x 2 + v y 2 + v z 2 ) ) − m g z ∂ v x \frac{\partial{(\frac{1}{2}m(v_x^2 + v_y^2 + v_z^2))} - mgz}{\partial{x}} = \frac{d}{dt}\frac{\partial{(\frac{1}{2}m(v_x^2 + v_y^2 + v_z^2))} - mgz}{\partial{v_x}} \\ ∂ x ∂ ( 2 1 m ( v x 2 + v y 2 + v z 2 ) ) − m g z = d t d ∂ v x ∂ ( 2 1 m ( v x 2 + v y 2 + v z 2 ) ) − m g z After having solved the partial derivatives, we end here because we already derived the equation of motion above (under Newton’s method):
d ( m v ⃗ ) d t = ( 0 0 − m g ) \frac{d(m\vec{v})}{dt} = \begin{pmatrix} 0 \\ 0 \\ -mg \end{pmatrix} d t d ( m v ) = ⎝ ⎛ 0 0 − m g ⎠ ⎞ To use the Hamiltonian method, we must first calculate the generalized momenta using the Lagrangian:
L = 1 2 m ( v x 2 + v y 2 + v z 2 ) − m g z ∵ p q = ∂ L ∂ v q p q = ∂ ( 1 2 m ( v x 2 + v y 2 + v z 2 ) ) − m g z ∂ v q p x = m v x p y = m v y p z = m v z ∴ v x = p x m ∴ v y = p y m ∴ v z = p z m L = \frac{1}{2}m(v_x^2 + v_y^2 + v_z^2) - mgz \\
\because p_q = \frac{\partial{L}}{\partial{v_q}} \\
p_q = \frac{\partial{(\frac{1}{2}m(v_x^2 + v_y^2 + v_z^2))} - mgz}{\partial{v_q}} \\
p_x = mv_x \\
p_y = mv_y \\
p_z = mv_z \\
\therefore v_x = \frac{p_x}{m} \\
\therefore v_y = \frac{p_y}{m} \\
\therefore v_z = \frac{p_z}{m} \\ L = 2 1 m ( v x 2 + v y 2 + v z 2 ) − m g z ∵ p q = ∂ v q ∂ L p q = ∂ v q ∂ ( 2 1 m ( v x 2 + v y 2 + v z 2 ) ) − m g z p x = m v x p y = m v y p z = m v z ∴ v x = m p x ∴ v y = m p y ∴ v z = m p z The Hamiltonian is described as:
H = p ⃗ ⋅ q ⃗ ˙ − L H = \vec{p} \cdot \dot{\vec{q}} - L \\ H = p ⋅ q ˙ − L Which means:
H = ( p x p x m + p y p y m + p z p z m ) − ( 1 2 m ( ( p x m ) 2 + ( p y m ) 2 + ( p z m ) 2 ) − m g z ) ∴ H = 1 2 ( p x 2 m + p y 2 m + p z 2 m ) + m g z H = (p_x\frac{p_x}{m} + p_y\frac{p_y}{m} + p_z\frac{p_z}{m}) - (\frac{1}{2}m((\frac{p_x}{m})^2 + (\frac{p_y}{m})^2 + (\frac{p_z}{m})^2) - mgz) \\
\therefore H = \frac{1}{2}(\frac{p_x^2}{m} + \frac{p_y^2}{m} + \frac{p_z^2}{m}) + mgz \\ H = ( p x m p x + p y m p y + p z m p z ) − ( 2 1 m ( ( m p x ) 2 + ( m p y ) 2 + ( m p z ) 2 ) − m g z ) ∴ H = 2 1 ( m p x 2 + m p y 2 + m p z 2 ) + m g z The Hamilton equations are:
d p q d t = − ∂ H ∂ q d q d t = ∂ H ∂ p q \frac{dp_q}{dt} = -\frac{\partial{H}}{\partial{q}} \\
\frac{dq}{dt} = \frac{\partial{H}}{\partial{p_q}} \\ d t d p q = − ∂ q ∂ H d t d q = ∂ p q ∂ H Therefore:
d p q d t = − ∂ H ∂ q = − ∂ ( 1 2 ( p x 2 m + p y 2 m + p z 2 m ) + m g z ) ∂ q
\frac{dp_q}{dt} = -\frac{\partial{H}}{\partial{q}} = -\frac{\partial{(\frac{1}{2}(\frac{p_x^2}{m} + \frac{p_y^2}{m} + \frac{p_z^2}{m}) + mgz)}}{\partial{q}} \\ d t d p q = − ∂ q ∂ H = − ∂ q ∂ ( 2 1 ( m p x 2 + m p y 2 + m p z 2 ) + m g z ) ( d p x d t d p y d t d p z d t ) = ( 0 0 − m g ) d q d t = ∂ H ∂ p q = ∂ ( 1 2 ( p x 2 m + p y 2 m + p z 2 m ) + m g z ) ∂ p q ( d x d t d y d t d z d t ) = ( p x m p y m p z m ) \begin{pmatrix} \frac{dp_x}{dt} \\ \frac{dp_y}{dt} \\ \frac{dp_z}{dt} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ -mg \end{pmatrix} \\
\frac{dq}{dt} = \frac{\partial{H}}{\partial{p_q}} = \frac{\partial{(\frac{1}{2}(\frac{p_x^2}{m} + \frac{p_y^2}{m} + \frac{p_z^2}{m}) + mgz)}}{\partial{p_q}} \\
\begin{pmatrix} \frac{dx}{dt} \\ \frac{dy}{dt} \\ \frac{dz}{dt} \end{pmatrix} = \begin{pmatrix} \frac{p_x}{m} \\ \frac{p_y}{m} \\ \frac{p_z}{m} \end{pmatrix} \\ ⎝ ⎛ d t d p x d t d p y d t d p z ⎠ ⎞ = ⎝ ⎛ 0 0 − m g ⎠ ⎞ d t d q = ∂ p q ∂ H = ∂ p q ∂ ( 2 1 ( m p x 2 + m p y 2 + m p z 2 ) + m g z ) ⎝ ⎛ d t d x d t d y d t d z ⎠ ⎞ = ⎝ ⎛ m p x m p y m p z ⎠ ⎞ Finally:
∴ ( d ( m d x d t ) d t d ( m d y d t ) d t d ( m d z d t ) d t ) = d ( m v ⃗ ) d t = ( 0 0 − m g ) \therefore \begin{pmatrix} \frac{d(m\frac{dx}{dt})}{dt} \\ \frac{d(m\frac{dy}{dt})}{dt} \\ \frac{d(m\frac{dz}{dt})}{dt} \end{pmatrix} = \frac{d(m\vec{v})}{dt} = \begin{pmatrix} 0 \\ 0 \\ -mg \end{pmatrix} ∴ ⎝ ⎜ ⎜ ⎛ d t d ( m d t d x ) d t d ( m d t d y ) d t d ( m d t d z ) ⎠ ⎟ ⎟ ⎞ = d t d ( m v ) = ⎝ ⎛ 0 0 − m g ⎠ ⎞ To conclude, the three methods are able to find the equation of motion. But, as you can probably tell, each method has its pros and cons. For example, the Newtonian method requires knowledge of each force acting on the ball. On the other hand, the Hamiltonian is really too wordy and annoying to solve.
The next steps are to understand how to simulate constraints using the Lagrange multiplier.