What is a hash table?
A hash table is a data structure that maps keys to values.

It is an unordered collection, because we use a hash function to distribute “evenly”** the elements in buckets (buckets) in an underlying data structure (such as for example an array ). ** I use quotation marks because it is not always uniform, as we will see.
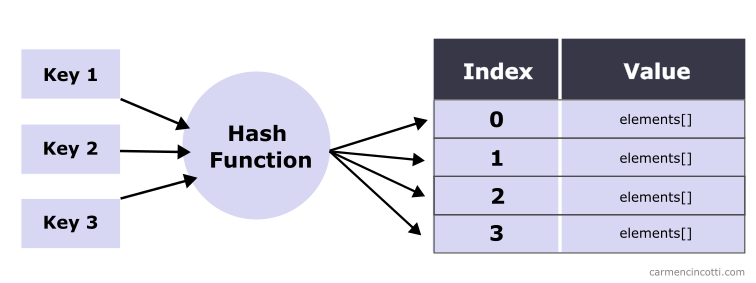
This uniform distribution is important because the goal is to reduce the search time to constant time .
An example
To see the usefulness of such a structure, let’s take this example. I have an array like this:

If I wanted to find if there is a in this array, I have to traverse it entirely.
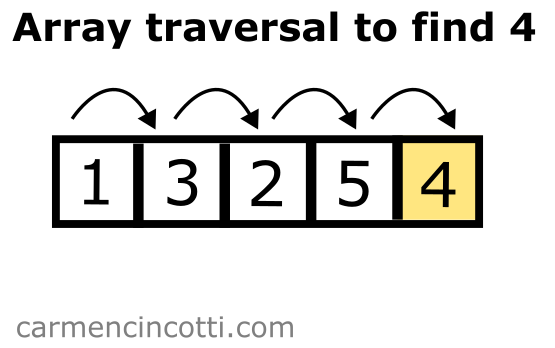
So it looks like the time complexity to search in such a structure is therefore on average, because we might have to traverse the entire array to finally find an element.
However, with a hash table that is well configured (with more buckets than elements), I could access such an element with constant time complexity on average.
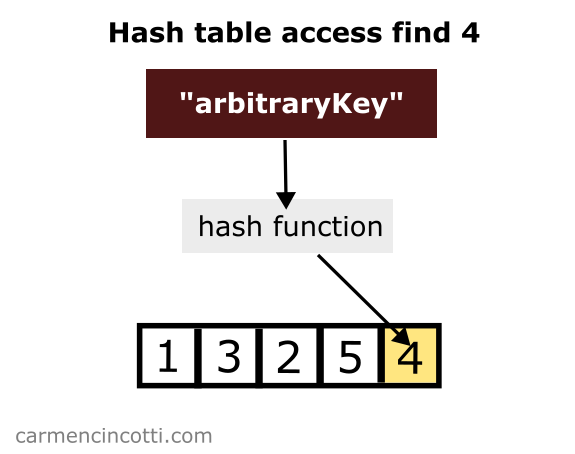
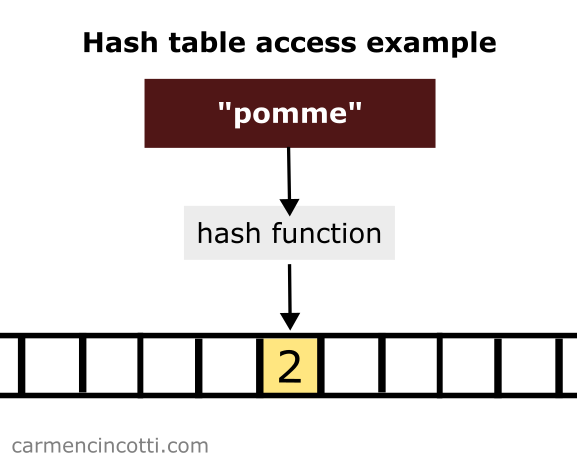
In the image above, we pass an arbitraryKey key to a hash function. The hash function returns us the index of the array to find .
The chances of accessing a bucket with a single element are high. We can say that on average, the time complexity to look up an element in a hash table is .
Hash collisions
However, there is a possibility that multiple keys are hashed to the same bucket.
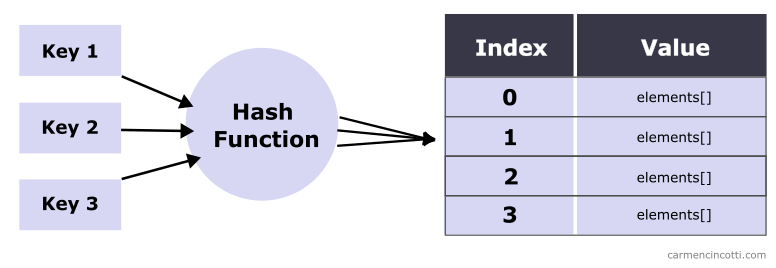
This phenomenon is caused by hash collisions which we will see together later.
That said, we can say that on average, the time complexity to look up an element is
Time complexity
To summarize, a hash table gives us more efficient time complexity compared to an array or a linked list when we would like to search, insert or delete an element (on average).
| Structure | Access | Search | Insertion | Deletion |
|---|---|---|---|---|
| Array | ||||
| Linked List | ||||
| Hash Table |
And in the worst case scenario, we would see these time complexities:
| Structure | Access | Search | Insertion | Deletion |
|---|---|---|---|---|
| Array | ||||
| Linked List | ||||
| Hash Table |
Why is there a worse case? This is due to hash collisions. Before seeing this phenomenon, we must first understand how a hash function works.
How to create a hash table
For those that are only interested in implementing these structures in code - I leave you some examples:
JavaScript
There are two ways to do this in JavaScript. With an Object type and a Map type.
const obj = {}
obj.name = "Carmen"
obj["name"] // Carmen
const map = new Map()
map.set("name", "Carmen")
map.get("name") // Carmen
What is the difference ? So all properties of type Object are modifiable, even those inherited by the base class Object - which makes this structure less secure.
For example, I could do the following:
const obj = {};
obj.name = "Carmen"
obj.hasOwnProperty = "Whoops"
obj.hasOwnProperty("name")
// ERROR: obj.hasOwnProperty is not a function
It is not possible to do this with Map.
Python
# Declare a dictionary
dictionary = {'Name': 'Carmen'}
dictionary["Name"] # Carmen
C++
std::unordered_map<std::string, std::string> u = {
{"Name","Carmen"},
};
u["Name"] // Carmen
Go
var m map[string]string
m = make(map[string]string)
m["name"] = "Carmen"
m["name"] // Carmen
The hash function
The hash function is a function that takes a key as input and returns us an index to access an element, a value, in a structure that we can index into (an array).

An input to the hash function can be anything. It’s the developer’s job to create a hash function that is able to hash the input type.
Imagine that I am selling fruit in a French supermarket. I have the following in stock:
| Fruit | Stock |
|---|---|
| Pomme | 2 |
| Pamplemousse | 4 |
I would like to access the stock of each fruit in constant time . This is a job for a hash table!
To do this, I create a hash function, hash as follows which takes a string key as input:
function hash(key: string): number {
var h = 0, l = key.length, i = 0;
if ( l > 0 )
while (i < l)
h = (h << 5) - h + key.charCodeAt(i++) | 0;
return h; // a number
}
If I use this function with an input like "pomme", I will see an output like 106849382 - which is the index we use to access the value in the array. Also, if I use "pamplemousse" - I will get 465401887.
With these indices - I could place the values in an array at these indices as follows:
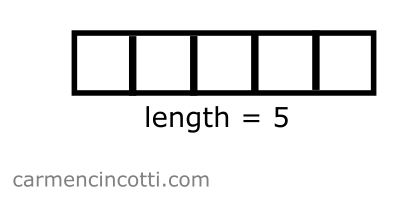
OK, but there is a small problem. With an index like 106849382, it looks like we need to have an array with a size of at least 106849382. This is too big just to store two values, even wasteful!
We also need to resolve the negative outputs of the hash function, since negative indices do not exist.
Moving forward, let’s imagine again that we would like to use a single array of size 5 elements to store our data.
Then I create a goodHash function that uses badHash, but I force the output to be positive and between
function badHash(key: string): number {
var h = 0, l = key.length, i = 0;
if ( l > 0 )
while (i < l)
h = (h << 5) - h + key.charCodeAt(i++) | 0;
return h; // a number
}
function goodHash(key: string): number {
var bad = badHash(key)
var arraySize = 5
return Math.abs(bad) % arraySize
}
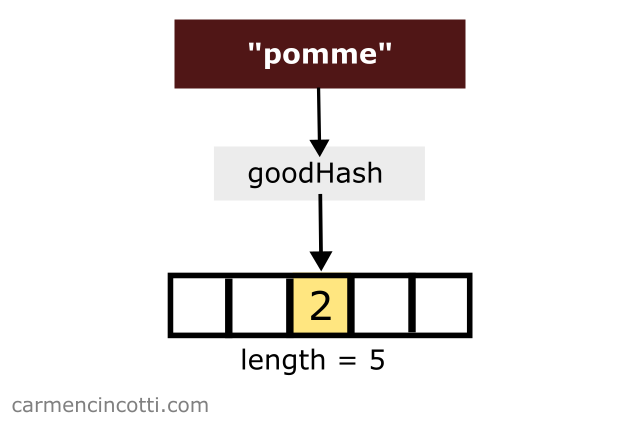
If I use "pomme" as input to the goodHash function, I will get as output. So I place the value of pomme in the bucket that corresponds to the index :
Then I do the same with the word pamplemousse. The goodHash function returns the same index, . What ?:
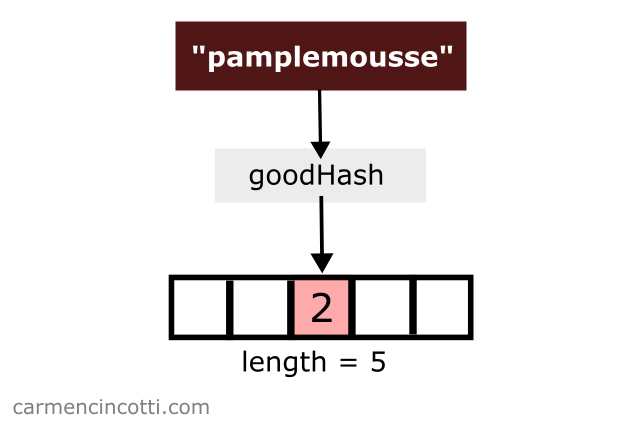
There is a problem! If I continue to place the value of pamplemousse in the array at index , I will overwrite the value of pomme!
This is called a hash collision !
Hash Collision - when a hash function returns the same index for multiple keys. There will be a “collision” between these two keys in the underlying storage structure.
This phenomenon deserves its own article. I’ll see you then!