Double hashing uses the idea of applying a second hash function to the key when a collision occurs in a hash table.
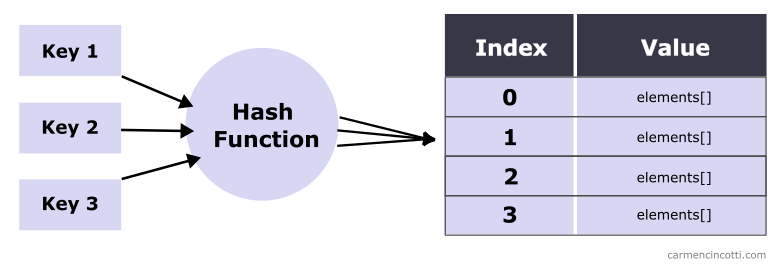
We’ll take a closer look at double hashing as well as how we can use it to resolve collisions when filling a hash table. We will also see that double hashing avoids problems encountered by other collision techniques, such as clustering.
Recall that last week we talked about quadratic probing, and before that linear probing, which are different methods used to resolve hash collisions in order to find and place items in a hash table.
That said, let’s dive into it by learning more about double hashing.
Hey! Before continuing on - if you haven’t already read the previous articles on open addressing and hash tables, I really recommend that you take a look so that you can more easily follow along:
What is Double Hashing?
Double Hashing is a way to resolve hash collisions by using a second hash function.
The formula
The double hashing formula for finding an open bucket or a particular element already placed in the hash table is the following:
where is the index of the underlying array, is the hash function, is the key of the element to be hashed. is the size of the table… and what about ?
is a second hash function (the double hash eh?). It is given the key of the element to hash. We multiply this number by which is the x-th iteration of the sequence.
Let’s take a look at what this means with an example.
An example
Consider an example using the hash function , and a table size . Assume is an integer.
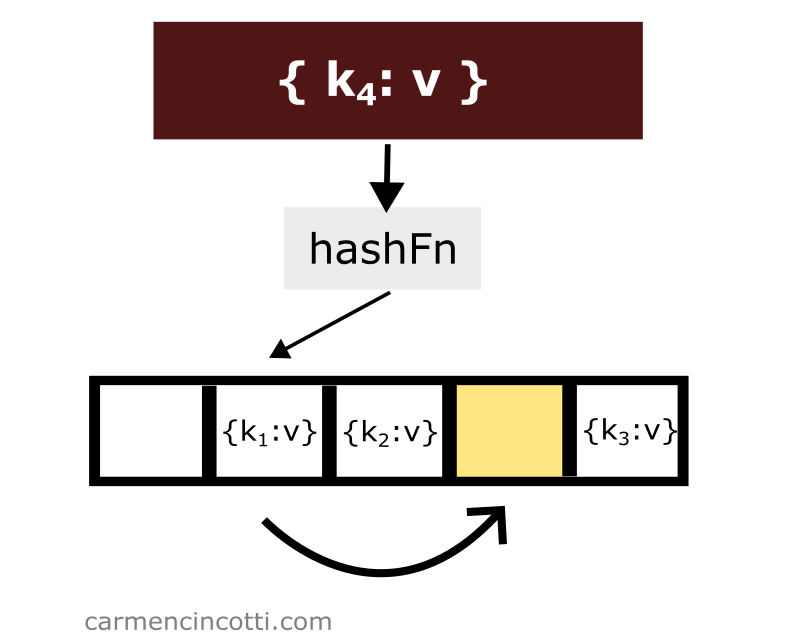
I also have a rather full hashtable, where the indices and in the underlying storage array are already occupied:
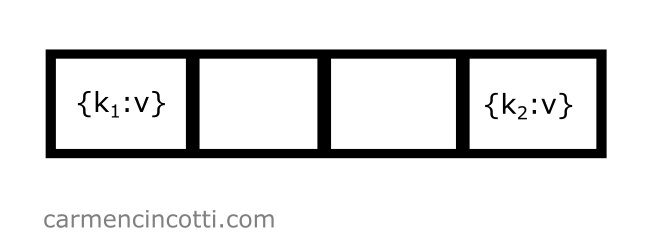
I would like to insert an element with a key, , which is hashed at index - so .
During our first iteration of the double hash sequence - we will see a formula filled in with the following values: , , , :
Our formula returns the index — but we have already seen that this location in the hash table is already occupied!
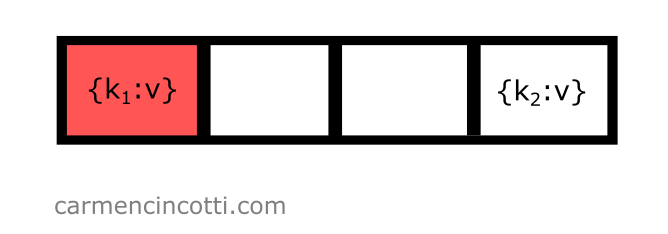
It’s necessary to try again to find an open bucket. Before continuing, we need to first iterate by . Doing this, we calculate like this: . Our next calculation of is as follows:
That’s it ! The probe found an open bucket at index :
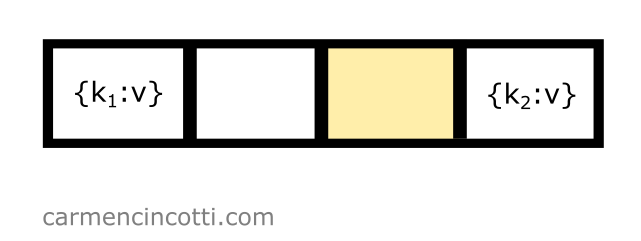
We’re done!
Cycles
Remember that a cycle is a series that never ends. This phenomenon occurs when a particular path is taken over and over endlessly when searching for an open bucket or an item already placed in the hash table.
To see how a cycle occurs I recommend you look at this example from my quadratic probing article.
Is double hashing susceptible to cycles?
Yes, double hashing is susceptible to cycles.
How can we avoid them?
A good way to avoid cycles is to carefully choose the second hash function, and the table size . TopCoder recommends that we use the following conditions to do this:
- is a prime number
- and
where is a second hash function.
The trick is that if those conditions are satisfied, we can ensure that the probing sequence is guaranteed to have order N, which makes us hit every bucket in our hash table.
Common operations
The common operations of a hash table that implements double hashing are similar to those of a hash table that implement other open address techniques such as linear or quadratic probing.
We will see what this means in the following sections.
Insertion
Inserting an item into a hash table using double hashing to resolve hash collisions is an easy task!
Consider the following example where we have an underlying array already populated with a few elements:
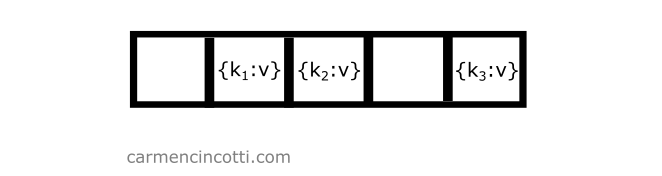
If we would like to add another element to the table with key which is hashed at the same location of another element, we only need to iterate through the underlying array until we find an open bucket in order to place the element in the table:

To do this, recall the formula . We iterate in order to traverse the array.
Search
The sequence defined by the double hash formula works like the probes we have already discussed. The underlying array is traversed looking for the element of interest:
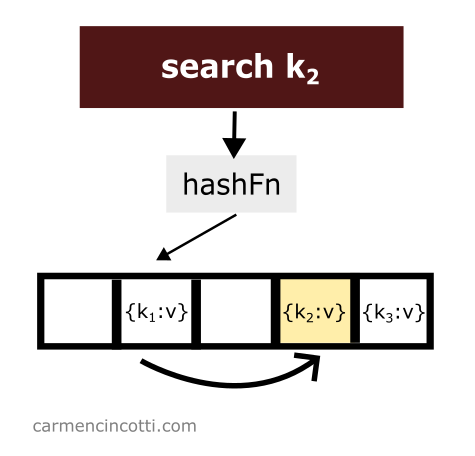
All is well if the item of interest is found!
However, if an empty bucket is found during the search, the search stops here. Nothing was found:
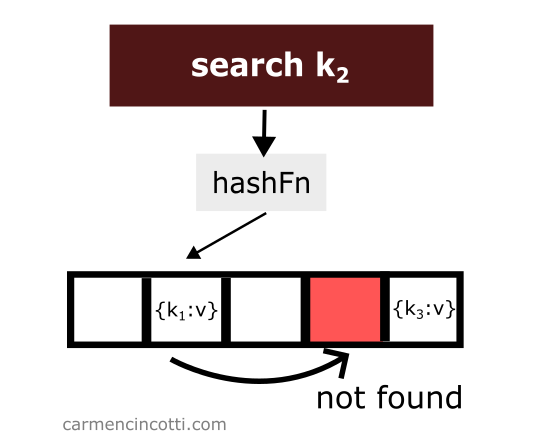
Which raises the question - what will happen if we delete an element? 🤔
Deletion
Deleting an item while using double hashing is a bit tricky. Consider this example where I naively remove an item from a hash table:
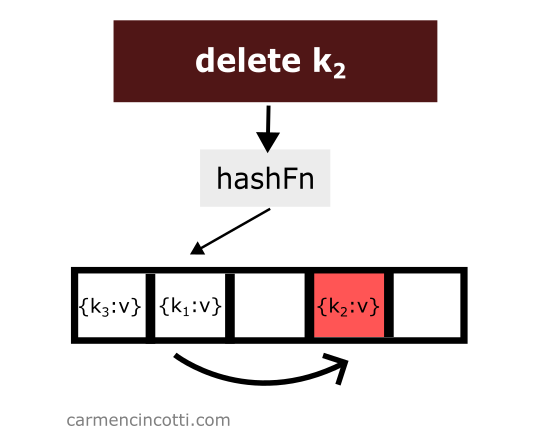
We just deleted an item from the hash table. Then we look for the item which is hashed by the hash function in the same location as the item which was just deleted and which was placed earlier in the hash table to the right relative to the element that has just been deleted:
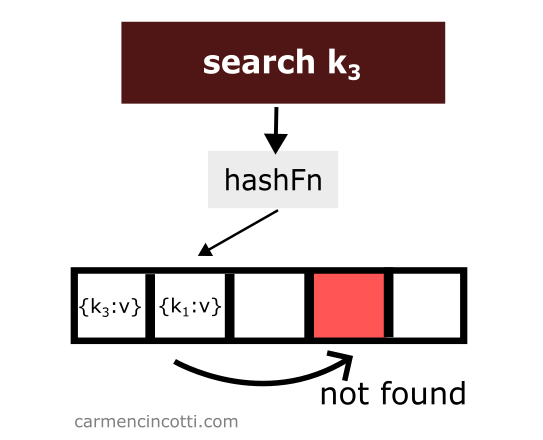
We won’t find it! Why? 🤔
Because the double hash sequence stops when it encounters an empty bucket.
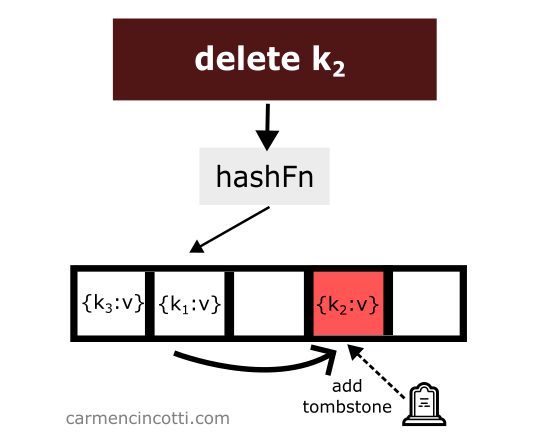
To avoid such unpredicted behavior - we must place at the location of the deletion of an element what is called a tombstone 🪦.
If the double hash sequence encounters a tombstone while searching the array, it will be ignored and the sequence will continue.
Let’s see an example with this idea in mind:
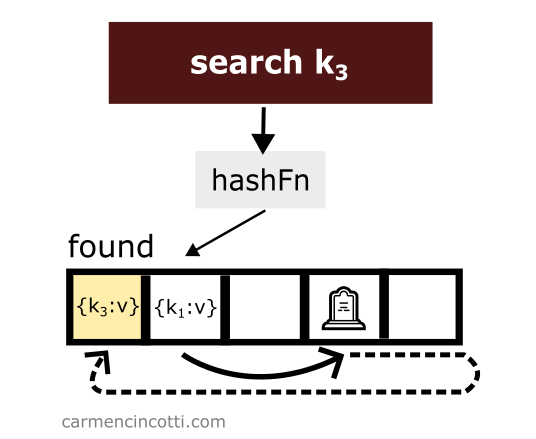
Then, we search for an element like before, however this time we are able to find it thanks to the tombstone:
Disadvantages
Although double hashing avoids clustering problems, it pays for this luxury by suffering from cache misses.
Cache performance
The double hash acts like a linked list. That is to say from the point of view of the CPU, the sequence is almost pseudo-random. This would make the cache almost useless…
Before we continue, it must be said that research suggests that double hashing is always better than linear probing, and even probing quadratic because it totally avoids clustering, which gives double hashing a real performance boost.
Advantages
Avoidance of clustering
Primary clustering
Fortunately, double hashing avoids primary clustering that we have already seen during our discussion of linear probing.
To summarize, primary clustering is a phenomenon that occurs when elements are added to a hash table. Elements can tend to clump together, form clusters, which over time will have a significant impact on the performance of finding and adding elements, as we will approach the worst case time complexity.
Secondary clustering
To sum up, secondary clustering happens when every new element that hashes to the same bucket in the table has to follow the same path each time, and thus must append itself to this to path when it finds an empty space… which will make this path grow over time and therefore further aggravate the problem.
Time complexity
To summarize, a hash table gives us more efficient time complexity compared to an array or a linked list when we would like to search, insert or delete an element (on average).
| Structure | Access | Search | Insertion | Deletion |
|---|---|---|---|---|
| Array | ||||
| Linked List | ||||
| Hash Table |
And in the worst case scenario, we would see these time complexities:
| Structure | Access | Search | Insertion | Deletion |
|---|---|---|---|---|
| Array | ||||
| Linked List | ||||
| Hash Table |
Why is there a worst case? This is due to hash collisions. One should choose an underlying array that is large enough as well as a rather moderate load factor.