This week, I would like to continue our conversation on open addressing and hash tables.
More specifically, we will take a closer look at quadratic probing and how we can use this technique when creating a hash table to squeeze every ounce of performance that we can out of our hash tables.
Recall that last week we talked about linear probing which is a good way to resolve hash collisions in order to find and place items in a hash table.
That said, let’s dive into it by learning more about quadratic probing.
Hey! Before continuing on - if you haven’t already read the previous articles on open addressing and hash tables, I really recommend that you take a look so that you can more easily follow along:
What is the difference between linear probing and quadratic probing?
Quadratic probing is not a technique where the probe traverses the underlying storage array in a linear fashion. Rather, it traverses the underlying storage array in a quadratic fashion.
For example - this is how the linear probe traverses the underlying storage array linearly when placing an item:
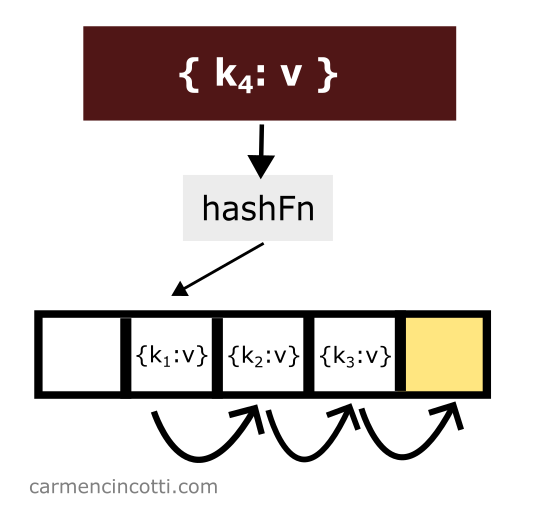
This concept of linearly traversing the underlying storage array is unique to linear probing…
We will see better how quadratic probing works during this article!
What is Quadratic Probing?
Quadratic Probing is a way to resolve hash collisions by quadratically searching for an open bucket, or a specific element until one is found.
The formula
The quadratic probing formula for finding an open bucket or a particular element already placed in the hash table is the following:
where is the index of the underlying array, is the hash function, is the key of the element to be hashed. is the size of the table… and ?
The new variable we need to get familiar with is . is the quadratic function we need to define and is the x-th probe iteration. Recall that a quadratic function takes the form: .
Let’s take a look at what this means with an example.
An example
Consider an example using the quadratic function , and a table size .
I also have a rather full hash table, where the indices and in the underlying storage array are already populated:

I’d like to insert an element that is hashed at index - so .
For our first probe iteration - we will see a formula filled in with the following values: , , :
Our formula returns the index — but we have already seen that this location in the hash table is already occupied!

It’s necessary to try again to find an open bucket. Before continuing, we need to first iterate by . Doing this, we calculate like this: . The probe is ready to try again:
That’s it ! The probe found an open bucket at index :

We’re done!
Cycles
The word cycle is defined by Vocabulary.com as follows:
Cycle: A cycle is a series of events that happen repeatedly in the same order.
As this definition suggests, a cycle never ends! This phenomenon occurs when a specific path is taken over and over again while searching for an open bucket or for an element that has been already placed in the hash table.
Let’s take a look at an example to really understand what this means.
An example
Let’s use the formula again:
In this example, I will be defining the quadratic function, , as , and the table size, , as .
I also have a rather full hash table, where the indices and are already populated:

I’d like to insert an element that is hashed at index - so .
For our first probe iteration - we will see a formula filled in with the following values: , , :
However, the index is not available, because an element is already there!

That said, we continue by increasing the value in order to find a free bucket.
| x | H(k) | J(x) | i |
|---|---|---|---|
| 0 | 0 | 4 | 0 |
| 1 | 0 | 6 | 2 |
| 2 | 0 | 12 | 0 |
| 3 | 0 | 22 | 2 |
| 4 | 0 | 36 | 0 |
| 5 | 0 | 54 | 2 |
The element is never placed because of a cycle!
You must therefore be careful to avoid such a phenomenon when choosing a quadratic function.
How to avoid a cycle
There are many methods and studies to find the best quadratic function. My research has concluded that there are fast and easy rules one can follow when starting out:
- , and keep the size of the table, , a prime number and also (the max load factor) <= .
- , and keep the size of the table a power of two: .
- , and keep the size of the table, , a prime number N where N ≡ 3 mod 4.
Common operations
The common operations of a hash table that implements quadratic probing are similar to those of a hash table that implements linear probing.
We will see what this means in the next sections.
Insertion
Consider the following example - we have an underlying array that is already populated with a few elements:
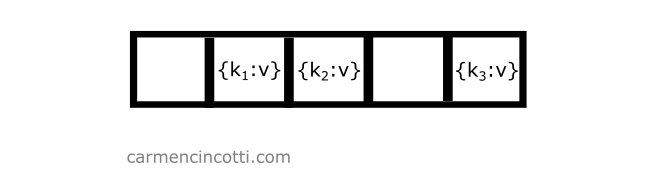
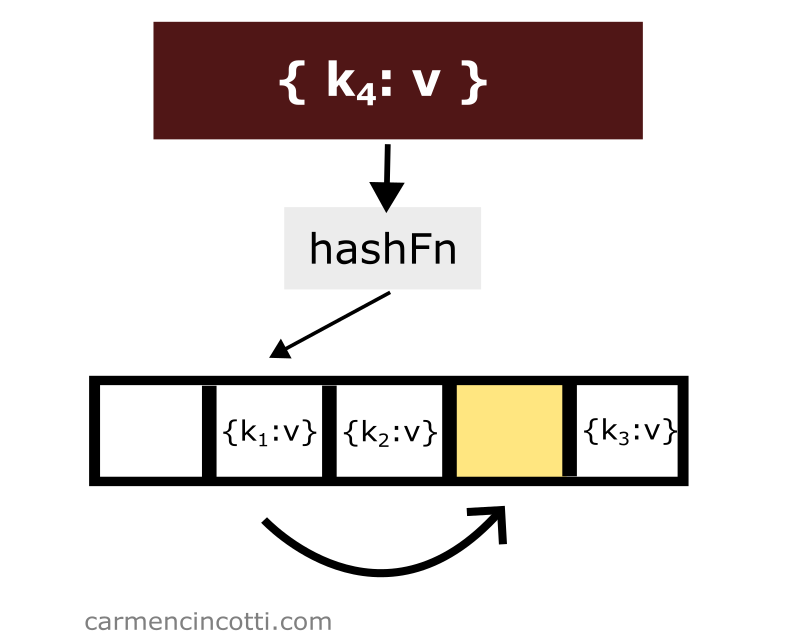
If we would like to add another element to the table with key which is hashed at the same location of another element, we only need to iterate through the underlying array until we find an open bucket in order to place the element in the table:

Search
Quadratic probing works as its name suggests. There is a probe that quadratically traverses the underlying array. If it finds an element in its path while traversing the array - it will return it to the user.
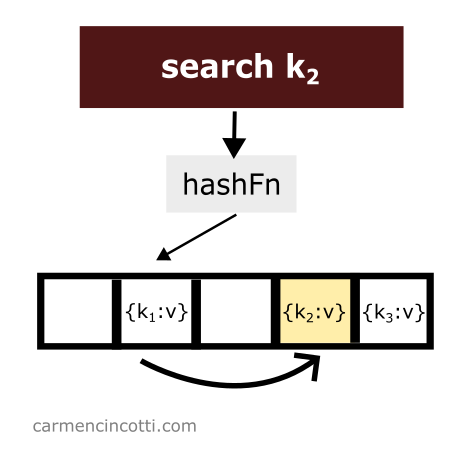
However, if it finds an empty bucket during its search, it will stop at this moment and signal to the user that it has found nothing.
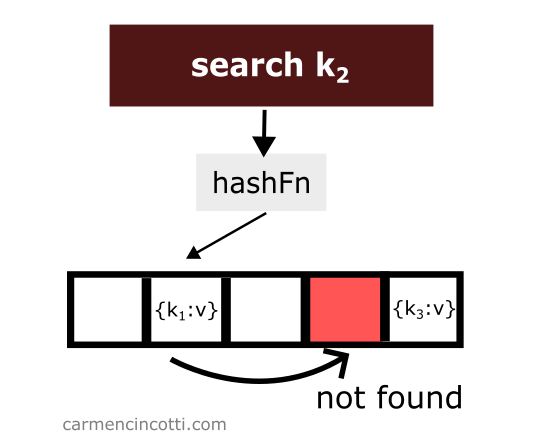
Which raises the question - what will happen if we delete an element? 🤔
Deletion
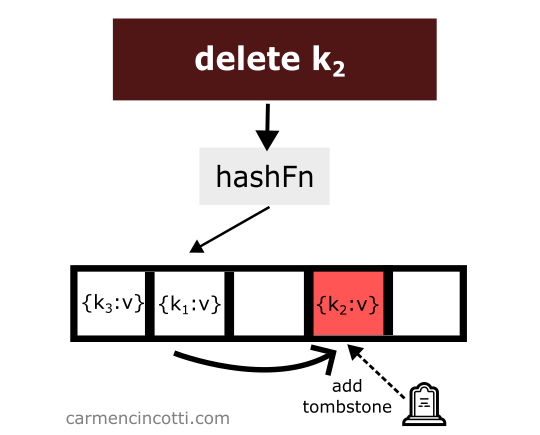
Deleting an item while using quadratic probing is a bit tricky. Consider this example where I naively remove an item from a hash table:
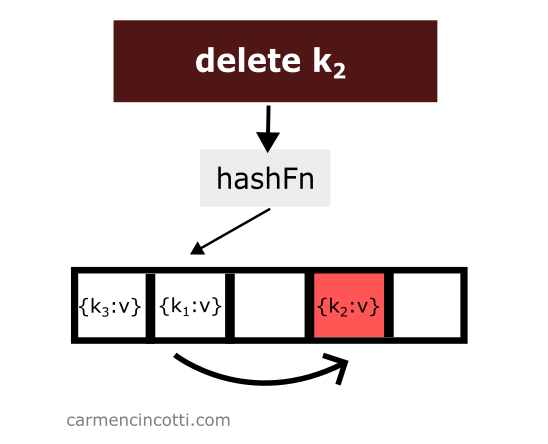
We just deleted an item from the hash table. Then we look for the item which is hashed by the hash function in the same location as the item which was just deleted and which was placed earlier in the hash table to the right relative to the element that has just been deleted:
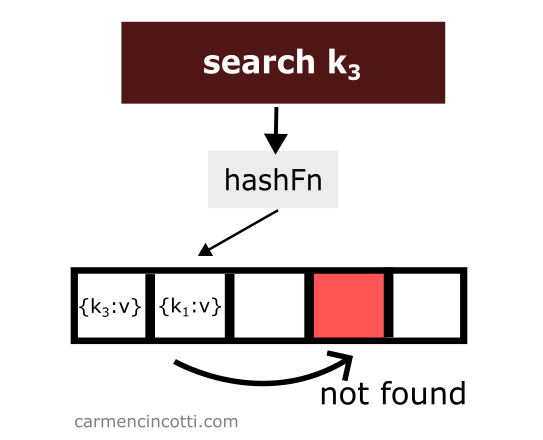
We won’t find it! Why? 🤔
Because the quadratic probe stops when it encounters a empty space.
To avoid such unpredicted behavior - we must place at the location of the deletion of an element what is called a tombstone 🪦.
If the quadratic probe encounters a tombstone while searching the array, it will ignore it, and continue its search for the element we want.
Let’s see an example with this idea in mind:
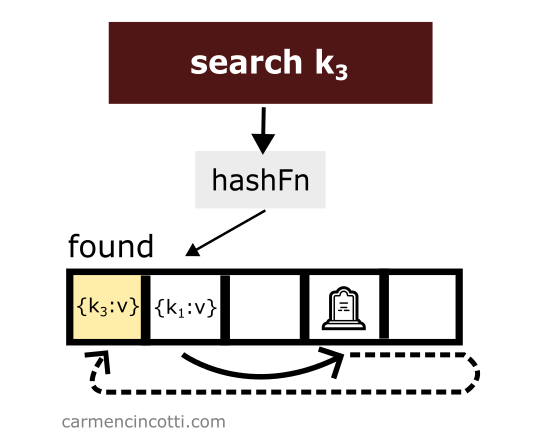
Then, we search for an element like before, however this time we are able to find it thanks to the tombstone:
Disadvantages
While quadratic probing avoids the primary clustering problems of linear probing, there is another less severe clustering - secondary clustering.
Secondary clustering
Secondary clustering is seen when filling a hash table with many elements that hash to the same open bucket.
For each element that initially hashes to the same bucket, the quadratic probe will deterministically visit the same buckets in order to find one that is open.
For each new element that hash to the same bucket into the table, it will be necessary to follow this path each time, and append the new element to this path… which will make this path grow over time and thus worsen the problem.
Cache performance
Moreover, we lose some cache efficiency due to the fact that to find a free space we have to traverse the array in a non-linear way.
Advantages
Primary clustering avoidance
Fortunately, quadratic probing is less sensitive to primary clustering that we have already seen during our discussion of linear probing.
To summarize, primary clustering is a phenomenon that occurs when elements are added to a hash table. Elements can tend to clump together, form clusters, which over time will have a significant impact on the performance of finding and adding elements, as we will approach the worst case time complexity.
Time complexity
To summarize, a hash table gives us more efficient time complexity compared to an array or a linked list when we would like to search, insert or delete an element (on average).
| Structure | Access | Search | Insertion | Deletion |
|---|---|---|---|---|
| Array | ||||
| Linked List | ||||
| Hash Table |
And in the worst case scenario, we would see these time complexities:
| Structure | Access | Search | Insertion | Deletion |
|---|---|---|---|---|
| Array | ||||
| Linked List | ||||
| Hash Table |
Why is there a worst case? This is due to hash collisions. One should choose an underlying array that is large enough as well as a rather moderate load factor.