Last week, we talked about hash tables in order to understand them better.

The goal is to eventually use a spatial hash table for our fabric simulation because we will have to use it to handle particle collisions.

When adding elements to such a structure, we have to be careful of hash collisions. Over the next few articles we will learn how to deal with them as they arise.

What is a hash collision?

A hash collision occurs when two or more keys are hashed at the same index of the underlying array of a hash table.

Without sufficient means to manage such a situation, we will have unexpected results.

Why is hash collision a problem?

Because we will overwrite existing data that already is stored in the hash table.

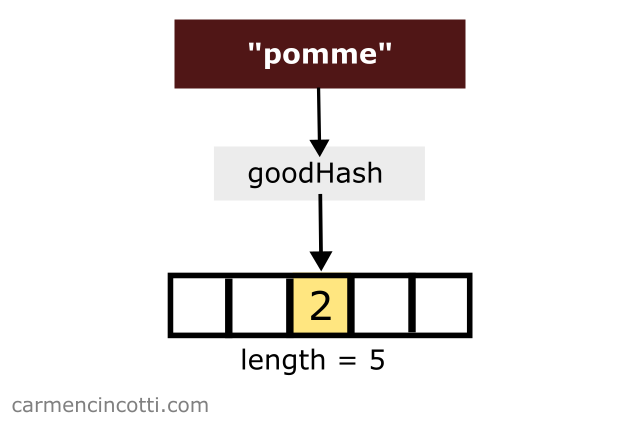
To illustrate such a situation, imagine that we would like to store the key-value pair { "pomme": 2 }. We have a hash function that hashes the key, pomme, to an index of $2$.

Next, we would like to store { "pamplemousse": 3} in our hash table. Coincidentally, the hash function hashes pamplemousse to an index of $2$… but the value of pamplemousse is already there!

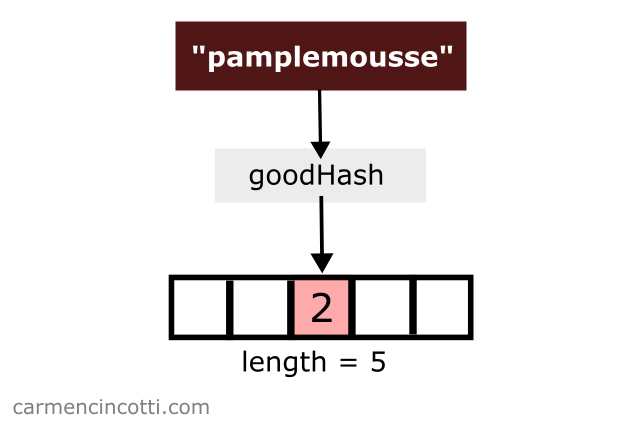
What can we do to handle this situation?

How do we handle a hash collision?

To resolve a hash collision, we have several options:

1. Separate Chaining - A linked list is used at each index in the array to store the data ​​of colliding keys.
2. Open Addressing - If a collision occurs, the array is searched to find an open bucket to store data. An additional data structure is not necessary.

The complexity of each method is measured by what is known as the load factor of the hash table. We will see this concept in the next article.

What is Separated Chaining?

Separate chaining is a way to resolve hash collisions in a hash table. Linked lists are placed at each index of the underlying array. Each key-value pair that matches an index in the array (after hashing the key) is added to the linked list.

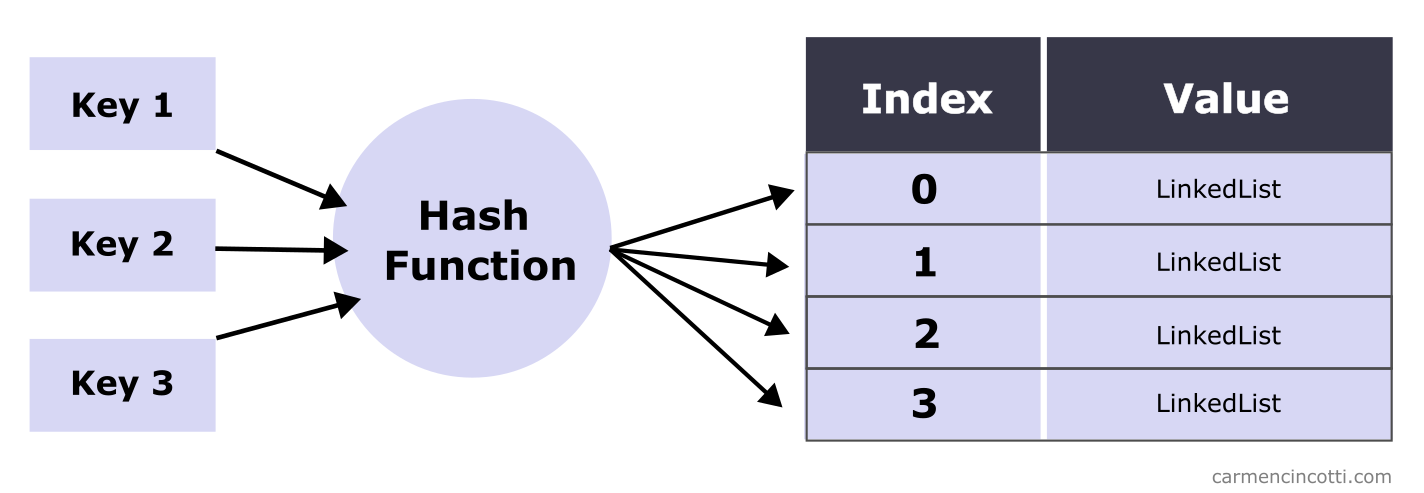
The time complexity for inserting, searching, and deleting on average trends toward $O(1)$ given that the underlying array is large enough to hold the unique elements we want to store, and that the hash function distributes the elements uniformly.

At the other extreme, the time complexity for these operations can resemble that of a linked list if the elements group together in a single bucket. That is, time complexity degrades to $O(n)$ for insertion, search, and deletion.

Separate chaining - how to insert an element?

Let’s imagine that there is a key-value pair { "key": 1 } which is hashed at index $4$. I could insert this pair by concatenating it to the linked list at that index like so:

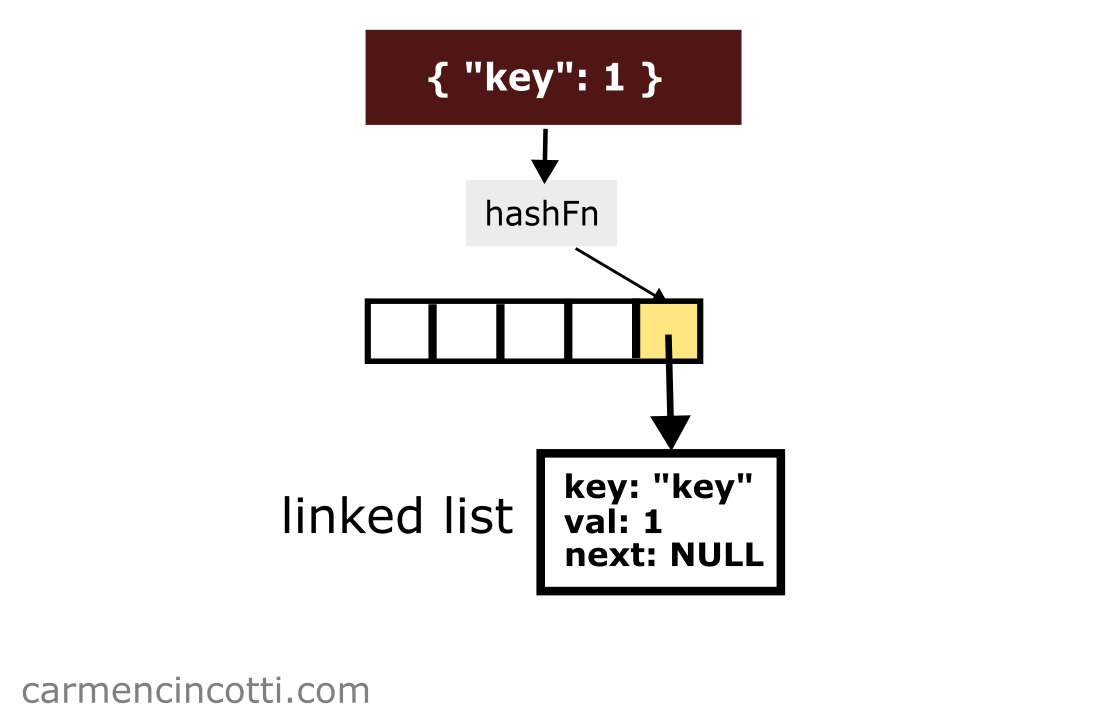
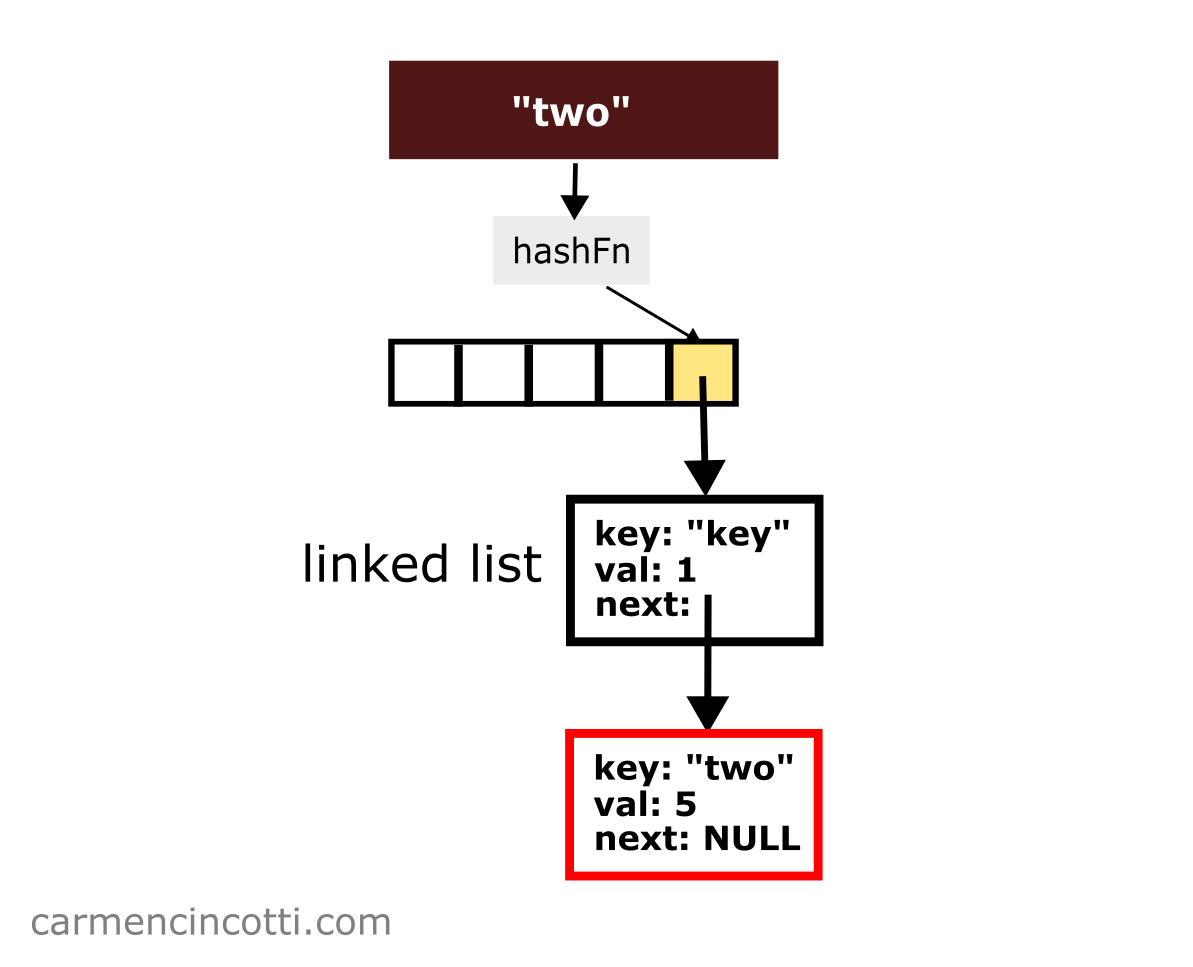
Next, imagine that I would like to insert the key-value pair { "two": 5 } which is hashed at the same index $4$ :

You just need to concatenate this new pair to the linked list!

Separate chaining - how to search for an element?

To find an element, we hash the key to find the index in the underlying array. Then, we traverse the linked list that is there. Using the key, we can visit and compare each node in the linked list until we find a match.

Of course - there’s the case where nothing is found. Each language handles this case differently. Maybe it’ll return ‘NULL’ or it may even throw an error.

Separate chaining - how to delete an element?

To delete an element, we do the same thing as to search for an element. Upon finding the node that matches the key, we remove it by disconnecting the node from the linked list.

What is the time complexity?

With the help of this strategy to resolve collisions, the time complexity to find, insert or delete an element (on average) is the following:

And in worst-case scenario, we would see these time complexities:

A worst-case scenario can be caused by an underlying array not being large enough. Another cause could be a hash function that creates groupings in a single bucket.

Next Time

Next week - we’ll look at open addressing, double hashing and load factor - stay tuned!

Resources

• Table de hachage - Developpez
• Separate Chaining - Scaler Topics
• Separate Chaining Collision Handling Technique in Hashing - Geeks for Geeks