Carmen's Graphics Blog

Computer Graphics and Physics Simulation Tutorials and Articles
PostsAboutProjectsJobs

The Distance Constraint | XPBD

XPBD uses particle constraints to ensure that particles move in a certain manner, relative to other particles. Let's take a deeper look into a common constrant that we'll find in a cloth simulation, the distance constraint.

Keywords: position based dynamics, cloth simulation, lagrange, physics, computer graphics

By Carmen Cincotti  

A big piece of the XPBD puzzle, which we already talked about a few weeks ago, is the satisfaction of particle constraints. Particle constraints force a particle to move in a certain way, relative to the other particles in the system.

How a particle moves back to the string

If you’ve been following me for the past few months, you most likely know of my goal to simulate fabric 🧵. Such a simulation may have complex constraints but for now we will only consider distance constraints and bending constraints.

Here are those famous articles that we already studied together during an article a few weeks ago on XPBD that I will reference for the math during this post:

A summary of XPBD

Recall that the XPBD algorithm with small steps is defined as follows:

Algorithm of XPBD with small steps

⚠️ As I said, we have already covered this algorithm thoroughly, and I recommend that you read the article if you are already lost.

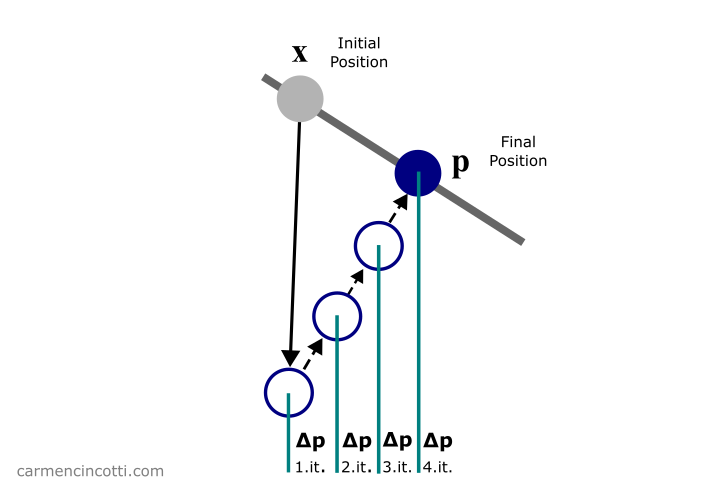
For now, we are only interested in the loop that is in lines (6) - (11). As you can see, the function of this loop is to satisfy the constraints of the simulation in order to directly correct the positions of each particle that participates in the constraints.

We just covered the reason why this simulation method is called as Position Based Dynamics - PBD 🎉.

Satisfying the constraints

Our objective during the loop is to calculate the correction vector that a particle must move in order to satisfy, or come closer to satisfying, the constraints.

Δx=ΔλM−1∇CxT\Delta \mathbf{x} = \Delta \lambda \mathbf{M}^{-1} \nabla C \mathbf{x}^T

where Δλ\Delta \lambda is defined as:

Δλ=−C(x)∇C(x)M−1∇C(x)T+α~\Delta \lambda = \frac{-C(\mathbf{x})}{\nabla C(\mathbf{x}) \mathbf{M}^{-1} \nabla C(\mathbf{x})^T + \tilde{\alpha}}

Note that α~=αΔt2\tilde{\alpha} = \frac{\alpha}{\Delta t^2} where α\alpha is the constraint compliance. Recall that α=1k\alpha = \frac{1}{k} where kk is the stiffness of the constraint. C(x)C(\mathbf{x}) is the constraint equation, ∇C(x)\nabla C(\mathbf{x}) is the gradient of ∇C(x)\nabla C(\mathbf{x}) and is therefore a vector. M−1\mathbf{M}^{-1} is a diagonal matrix of inverse masses of the particles participating in the constraint.

Δλ\Delta \lambda, C(x)C(\mathbf{x}), and α~\tilde{\alpha} are scalar values.

Using these equations, we will simulate some constraints with code! 🖥️

The distance constraint

To start, we will talk about the distance constraint because it is rather easy to understand. The objective is to satisfy the constraint by moving two particles so that they approach each other at the rest length, dd:

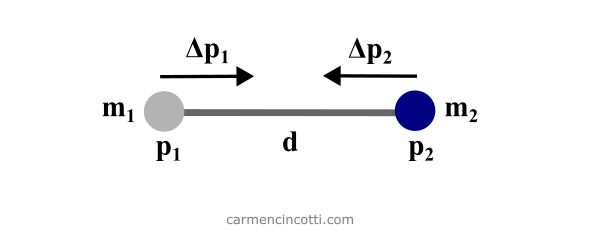
Distance constraint

where pp is the position of a particle and mm is the mass.

We can solve the equations from the last section in order to find the final position corrections, Δxn\Delta \mathbf{x}_n :

C(x1,x2)=∣x1,2∣−dn=x1,2∣x1,2∣Δx1C(x1,x2)=nΔx2C(x1,x2)=−n∴Δx1=−w1w1+w2(∣x1,2∣−d)n∴Δx2=+w2w1+w2(∣x1,2∣−d)n C(\mathbf{x_1}, \mathbf{x_2}) = |\mathbf{x}_{1,2}| - d\\[6pt] \mathbf{n} = \frac{\mathbf{x}_{1,2}}{|\mathbf{x}_{1,2}|}\\[6pt] \Delta_{\mathbf{x_1}}C(\mathbf{x_1}, \mathbf{x_2}) = \mathbf{n}\\[6pt] \Delta_{\mathbf{x_2}}C(\mathbf{x_1}, \mathbf{x_2}) = -\mathbf{n}\\[6pt] \therefore \Delta \mathbf{x_1} = - \frac{w_1}{w_1 + w_2}(|\mathbf{x}_{1,2}| - d) \mathbf{n}\\[6pt] \therefore \Delta \mathbf{x_2} = + \frac{w_2}{w_1 + w_2}(|\mathbf{x}_{1,2}| - d) \mathbf{n}\\[6pt]

The code solution

Here is the code where I define two particles. The distanceConstraint function is based on calculating Δλ\Delta \lambda and immediately updating the position, pp of the particle pnp_{n}. There is a distance constraint with rest length equal to 11.

You may notice that there is a little trick during the calculation. Recall that the calculation to find Δλ\Delta \lambda is:

Δλ=−C(x)∇C(x)M−1∇C(x)T+α~\Delta \lambda = \frac{-C(\mathbf{x})}{\nabla C(\mathbf{x}) \mathbf{M}^{-1} \nabla C(\mathbf{x})^T + \tilde{\alpha}}

Fortunately, ∇C(x)\nabla C(\mathbf{x}) is a normalized vector. So:

∇C(x)T∇C(x)=1\nabla C(\mathbf{x})^T\nabla C(\mathbf{x}) = 1

We can therefore simplify our equation as follows:

Δλ=−C(x)M−1+α~\Delta \lambda = \frac{-C(\mathbf{x})}{\mathbf{M}^{-1} + \tilde{\alpha}}

Finally, I used a logging function to see how the particles move before and after the simulation loop:

BEFORE APPLYING XPBD LOOP ------------------------- POSITION P1: [ '2.0000', '2.0000', '0.0000' ] POSITION P2: [ '-2.0000', '-2.0000', '0.0000' ] AFTER APPLYING XPBD LOOP ------------------------ POSITION P1: [ '0.3536', '0.3536', '0.0000' ] POSITION P2: [ '-0.3536', '-0.3536', '0.0000' ]

We see that the two particles approach each other and move to the points p1=(.3536,.3536,0),p2=(−.3536,−.3536,0)p_1 = (.3536, .3536, 0), p_2 = (-.3536, -.3536, 0). Do these new points satisfy the distance constraint? Recall that the length of rest is equal to 11:

.35362+.35362+.35362+.35362≈1\sqrt{.3536^2 + .3536^2} + \sqrt{.3536^2 + .3536^2} \\[6pt] \approx 1

Yes! The distance constraint has been satisfied!

Next time

We will see together the isometric bending constraint. Stay tuned!

Resources

Comments for The Distance Constraint | XPBD

Written by Carmen Cincotti, computer graphics enthusiast, language learner, and improv actor currently living in San Francisco, CA.  Follow @CarmenCincotti

Contribute

Interested in contributing to Carmen's Graphics Blog? Click here for details!